Inscription / Connexion Nouveau Sujet
similitudes
Salut
ABCD étant un rectangle de centre O tel que et AB=1 et AD=2. On pose E et F les milieux respectifs des segments [AD] et [BC].
Soit f la similitude directe telle que f(A)=F et f(B)=D.
1) Déterminer le rapport et l'angle de f.
2) Déterminer f((BC)).
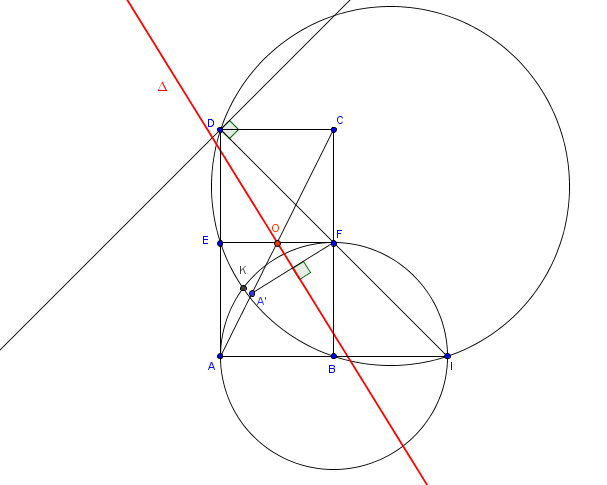
3) Soit {I}=(AB)
(DF) et K le centre de f. Montrer que K appartient aux cercles circonscrits aux triangles IAF et IBD. Construire alors K.
4) Soit g la similitude directe de centre F telle que g(B)=D. Caractériser h=f°g-1.
5) Soit S la similitude indirecte telle que S(A)=F et S(C)=E. Caractériser S.
1) k=
2
=-
/4.
2) f((BC)) est la droite passant par D et 
(FD).
4)h est la rotation de centre F et d'angle -/2.
je n'arrive pas à répondre à la dernière question 5.
Merci
édit Océane : niveau modifié
Bonjour,
Il y a des choses qui ne vont pas:
1) k=
2
=-/4.Non,
4)h est la rotation de centre F et d'angle -
/2.Non, son centre est
5) Son rapport vaut
Comme ce n' est pas une isométrie, elle a un unique point invariant.
Pour le trouver, on peut se souvenir qu' une similitude conserve les milieux.
Soit le milieu de
Son image par sera le milieu de
, c' est à dire
L' unique point invariant de est donc le centre du rectangle
Je ne vois pas bien ce qu' on peut dire de plus...
J' aimerais savoir comment tu définis l' axe d' une similitude indirecte de rapport différent de 1 ?
alors on n'a besoin que du rapport et du centre pour déterminer les caractéristiques d'une similitude indirecte?
Dans le cas d' une similitude indirecte, 2 cas peuvent se présenter:
Ou bien son rapport est 1 et c' est un antidéplacement (symétrie ou symétrie glissée) et là on peut parler d' axe.
Ou bien son rapport est différent de 1 et la notion d' axe n' a plus grande signification. Par contre dans ce cas là, on a un unique point invariant (celui que tu appelles "centre")
Mais peu être as-tu étudié les similitudes hors de France avec une définition d' axe étendue ?
Après recherches, je viens de voir ceci (je ne connaissais pas la seconde partie):
Toute similitude indirecte de rapport et de centre
se décompose d'une manière unique en composée commutative d'une homothétie de centre
et d'une symétrie orthogonale d'axe passant par
L'axe d' une similitude indirecte de centre et de rapport
est l'ensemble des points
d'image
tel que
Vu sous cet angle, toute similitude indirecte a un axe...
Au vu de ce qui est écrit au dessus, voici l' "axe" de :
se décompose donc de manière unique en produit commutatif de l' homothétie
de centre
, de rapport
et de la symétrie orthogonale d' axe
passant par
à déterminer.
Or soit
Soit : on a
est donc la médiatrice de
:
Merci pour toutes ces clarifications, ça m'a beaucoup aidé.
6) Le plan étant rapporté à un repère orthonormé direct . Pour tout point M(z) on pose M'(z') tel que f(M)=M'.
Exprimer z' en fonction de z. En déduire les coordonnées de K.
Que dois-je faire?
Merci pour toutes ces clarifications, ça m'a beaucoup aidé.
J' en suis bien content
6)
Son écriture complexe est
On a dans le repère
d' où le système:
qui donne
L' écriture complexe de
Pour trouver les coordonnées (ou l' affixe) de
On résout donc l' équation
On trouve
la dernière question: En déduire l'ensemble C des points M(z) tels que:
j'ai trouvé qu'il s'agissait du cercle de centre E et de rayon 1
j'ai trouvé qu'il s'agissait du cercle de centre E et de rayon 1
C' est juste mais ce résultat s' obtient sans calculs; j' espère que tu n' en a pas fait...
Annuler
connectez vous