Inscription / Connexion Nouveau Sujet
simple à comprendre mais difficile à démontrer...
pouvez vous m'aider car je bloque sur cette démonstration peu commode :
Soit A B C un triangle,
le point D est l'intersection de la bissectrice de  avec le coté BC
le point E est l'intersection de la bissectrice de ^B avec le coté AC
le point F est l'intersection de la bissectrice de ^C avec le coté AB
La mediatrice du segment AD coupe BC en L
La mediatrice du segment BE coupe AC en M
La mediatrice du segment CF coupe AB en N
démontrer que L, M, N sont alignés.
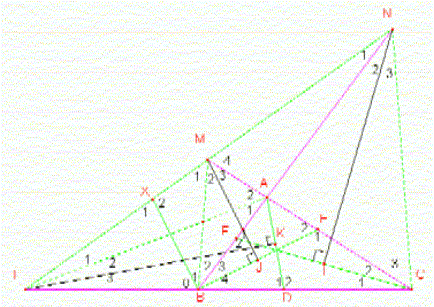
Cette démonstration ne fait pas intervenir d'élément bien compliqué (med et biss) mais je n'arrive pas à y arriver au bout, voici le shéma:
rebonjour à tous,
cet exercice n'inspire t-il personne? personne ne pourrait me donner ne serat-ce q'une piste...?
merci à tous...
Bonsoir Al-khwarizmi !
Voici une piste possible.
Tu peux calculer trois angles consécutifs de sommet M et prouver que leur somme vaut 180°.
Pour l'un d'eux, tu dois tenir compte que M est équidistant de B et de E et travailler à partir du triangle isocèle MBE.
Pour les autres, tu dois travailler avec les bissectrices extérieures du triangle ABC aux sommets B et C. Par exemple, la bissectrice extérieure en C est parallèle à la médiatrice de CF.
Essaie et tiens-moi au courant !
Au plaisir.
Bonjour
Voici un dessin qui permettra d'y voir plus clair car moi je tourne en rond.
Avec les relations qui suivent (faciles à montrer) il faudrait en arriver à ce que L1+N1=C (=C2+C3) ou M1+M4=2C+B (B=B3+B4) pour que M1+M2+M3+M4 = pi
BX est la bissectrice extérieure de B donc perpendiculaire à BE et // MJ
M2+M3=2M2=A-C ;L2+L3=2L2=B-C ; N2+N3=2N2=A-B
L1+M1=2C ;N1+M4=pi-A ;B0+B1=A
B2=C ; A2=B ;A1=C
M2=B1 ;X1=M1+M2
Bon courage
A plus geo3 
Saluuut
Merci tt le monde, je vais réflécr à vos proposition.
Je vous tiens a courant, promis.
Bonne semaine à tous.
*
Une propriété des pieds des bissectrices issues de A :
(B;C;D;K) est une division harmonique.
En déduire que LB/LC=DB²/DC²
*
Une propriété du pied de la bissectrice :
DB/DC=AB/AC
*
Donc LB/LC=AB²/AC²
*
Relations analogues pour M et N.
Le théorème de Menelaus permet de conclure.
A vérifier...
Bonjour
L n'est pas le pied de la bissectrice extérieure issue de A mais appartient à la médiatrice de [AD].
Evidemment si LB/LC=AB²/AC² alors le tour est joué.
Mais maintenant je sens qu'il faut plus se diriger vers des rapports et Menelaus ( que je croyais ne pas devoir employer car méconnu du candidat)
A plus geo3 
Bonjour
L n'est pas le pied de la bissectrice extérieure issue de A mais appartient à la médiatrice de [AD].(dommage)
Evidemment si LB/LC=AB²/AC² alors le tour est joué.
Mais maintenant je sens qu'il faut plus se diriger vers des rapports et Menelaus ( que je croyais ne pas devoir employer car méconnu du candidat)
A plus geo3 
Dans mon texte, K est le pied de la bissectrice extérieure et L est le milieu de [KD].
De vieux souvenirs sur la division harmonique
Rebonjour
Avant propos
Pour le topic 67397 j'avais employé en 3,4 lignes les théorèmes de Ménélaus et Céva pour arriver à la thèse mais le candidat n'en connaissait rien alors je me suis basé sur la théorie des barycentres beaucoup plus longue qui m'a donné presque la solution sauf une erreur de signe que je n'ai pas encore su déceler ( cf . topic 68332).
C'est ainsi qu'ici je me suis acharné (ç'est un défaut comme une qualité) sur la méthode angulaire qui n'a pas abouti ( on devrait pourtant peut-être savoir y parvenir).
Merci à Dasson de m'avoir remis sur rail ou dans le "droit chemin ".
Les pieds D et K des bissectrices issues de A partage effectivement harmoniquement B et C et (BCDK) est un quaterne harmonique.
Si L est le milieu de KD ,DK = 2DL et on peut en déduire que LB/LC=DB²/DC² (démonstration ci-dessous)(*)
*
Le 1er théorème de la bissectrice dit que : DB/DC=AB/AC
Donc LB/LC=AB²/AC² ; de même MC/MA = BC²/BA² et NA/NB = CA²/CB²
Dès lors BL/LC . CM/MA . AN/NB = (-AB²/AC²).(-BC²/BA²).(-CA²/CB²) = -1 =>
d'après la réciproque de Ménélaus L, M et N sont alignés.c.q.f.d.
Démonstration de (*)
LB/LC = DB²/DC² <=> LB/LC = (LB-LD)²/(LC-LD)² <=> ...<=> LC.LB(LC-LB) = LD²(LC-LB) <=> LC.LB = LD² (=LK²) <=>
(LC+DC).(LD+DB) = LD² <=> LD.(DC+DB) + DC.DB = 0 <=> 1/DL = (DC+DB)/(DC.DB) <=> 2/DK = 1/DB + 1/DC <=> 1/DK - 1/DB = -1/DK + 1/DC <=>
(DB-DK)/(DK.DB) = -(DC-DK)/(DK.DC) <=> KB/DB = - KC/DC <=> (BD/DC)/(BK/KC) = -1
<=> BCDK est un quaterne harmonique ( ouf il suffit d'y croire)
Encore merci à Dasson.
A plus geo3 


 géométrie en post-bac
géométrie en post-bac