Inscription / Connexion Nouveau Sujet
Nightmare
Cette inégalité est au programme de première
et les primitives sont au programme de terminale
jean-émile
Nightmare
Cette double inégalité sert à calculer la limite de sin(x)/x en 0 , c'est-à-dire la valeur de la dérivée de la fonction sinus en 0 en classe de Première
jean-émile
En effet pour montrer que sin est dérivable sur  et a pour dérivée cos , on a besoin de la limite de sin(h)/h en 0
et a pour dérivée cos , on a besoin de la limite de sin(h)/h en 0
jean-émile
Donc j'ai "rien" à faire, je commence à me perdre un peu là 
Je vous remercie, j'ai déjà bien appris !
amicalement.
Erwan
>jean émile
Très belle démonstration que celle fournie à 18:21
Accessible et très "visuelle"...
Merci
Philoux
Erwan
onc j'ai "rien" à faire, je commence à me perdre un peu là
Effectivement, avec une fonction composée de segments de droite, calculer les pentes des 1/2 tangentes a peu d'intérêt.
Si tu le veux, tu peux continuer ta résolution de la fonction proposée à 17:30 :
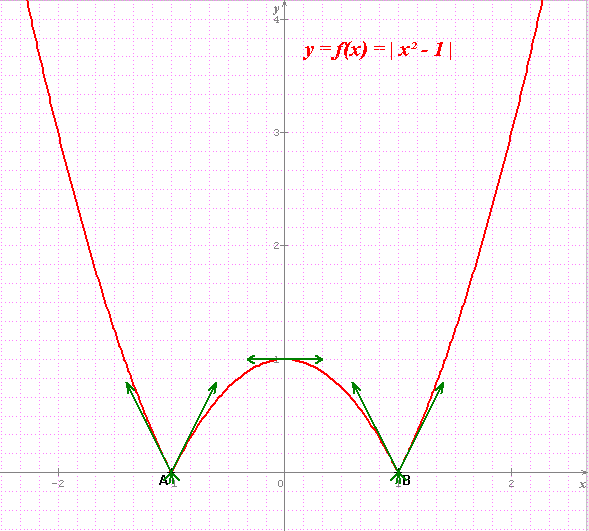
y = f(x) = |x²-1|
Quelles sont les pentes des deux 1/2 tangentes aux points A(-1,0) et B(1,0) ?
Tu étais bien parti avec ton post de 18:08
essaies de faire l'étude complète avec les deux 1/2 tangentes aux points A(-1,0) et B(1,0).
Philoux

Voici ce que j'ai fais :
_ signe de x²-1 :
 + sur ]-
+ sur ]-;-1[
 ]1;+
]1;+[.
 - sur [-1;1].
- sur [-1;1].
_ Sachant que :
 |x| = x , si x
|x| = x , si x 0.
0.
 |x| = -x , si x
|x| = -x , si x 0.
0.
_ On en déduit que :
 |x²-1| = x²-1 , si x²-1
|x²-1| = x²-1 , si x²-1 0.
0.
 |x²-1| = -(x²-1) = -x²+1 , si x²-1
|x²-1| = -(x²-1) = -x²+1 , si x²-1 0.
0.
D'où:
 Sur ]-
Sur ]-;-1[
 ]1;+
]1;+ : x²-1 > 0.
Or A(-1;0) :
donc : f'(-1) = -2 et f(-1) = 0.
D'après l'équation de la tangente ( y= f'(a)(x-a)+ f(a) ) on a :
yA = -2x-2.
-2 est le coefficient directeur, c'est à dire la pente de la 1/2 tangente.
 [-1;1] : x²-1 < 0.
[-1;1] : x²-1 < 0.
Par suite, |x²-1| = -x²+1.
Donc f'(-1) = 2 et f(-1)= 0.
Soit yA = 2x+2.
Par conséquent le coefficient directeur 2 définit la pente de cette 1/2 tangente.
De même avec B(1;0) on trouve :
 Sur l'intervalle où x²-1 est + :
Sur l'intervalle où x²-1 est + :
une demi tangente d'équation yB = 2x+2.
et sur [-1;1] :
une demi tangente d'équation yB = -2x-2.
Voilà mon travail.
Merci

@+
Erwan
Re 
Je ne comprend pas les enchainements logiques ...
d'où vient le "d'où" du quatriéme paragraphe ? Cela n'est aucunement impliqué du paragraphe d'avant !
Pareillement dans le premier paragraphe , tu fais une étude de signe mais tu ne t'en sers pas 
(en effet , il n'y avait pas besoin d'étudier le signe de x²-1 pour savoir que
|x²-1| = x²-1 , si x²-1<0.
|x²-1| = -(x²-1) = -x²+1 , si x²-1>0)
Ce que tu dois arriver à faire , c'est écrire :
Recommence

Jord
Erwan 14:25
Pas mal tout ça.
La courbe en image jointe.
On continue ?
Peux-tu alors "discuter" selon la valeur de m, le nombre et le signe des solutions de l'équation :
| x² - 1 | = m
Philoux
Nightmare :
> je suis d'accord pour le "où" qui n'avait rien à faire là 
néanmoins je réutilise le signe dans le 4ème paragraphe ?!et dans le 8ème ?! j'ai du mal à comprendre..
PS : Comment tape-on les valeurs absolues sur une Ti 82 ?
Mes demi-tangentes sont-elles bonnes
Tant que c'est des maths, je continue 
>erwan
Mes demi-tangentes sont-elles bonnes
seules les pentes 2 et -2 étaient demandées 
Philoux
Tu ne vois pas que c'est inutile de dire :
?

Nous ce qu'on veut c'est savoir ce que va valoir |x²-1| suivant la valeur de x et non la valeur de x²-1
Tu vois ce que je veux dire ?
ah ok...je comprends un peu mieux, je vais essayer de reprendre ce que t'as demandé dans ton post précédent  et après la courbe de Philoux.
et après la courbe de Philoux.
Ce que je fais est-il au programme de 1ère ?
Si je m'en réfère à la définition, j'obtiens :
|x²-1| = -x²+1 si x 0.
0.
|x²-1| = x²-1 si x 0.
0.
mais je ne suis pas convaincu 
Skops : merci, "abs(" ? je n'ai pas 
erwan 15:19
Verifies
|x²-1| = -x²+1 si [-1;+1]
...
Philoux
skops > j'ai : round( ; ipart; fpart ; int ; min( ; max(...
je trouve pas..enfin c'est pas grave, c'est pas ma priorité la calculette 
si je prends x 0 mais dans l'intervalle [-1;+1],
0 mais dans l'intervalle [-1;+1],
bon j'ai pris x = 0,5.
je devrais avoir :
|x²-1| = - (x²-1).
je remplace x par 0,5 dans le membre de droite et j'obtiens bien un nombre positif (0,75)...donc çà semble coordonner.
>erwan 15:43
Essaies de tenir compte des remarques de Nightmare sur la rigueur à avoir dans la rédaction.
On voit que, grosso modo, tu as compris ( le "pas mal tout ça" de 14:50  ), mais ta rédaction est approximative.
), mais ta rédaction est approximative.
Tu continues sur le post de 14:50 ?
Philoux
je viens de remarquer que si je prends x = -2, j'obtiens :
-[(-2)²-1] = - 3 , remarque : ce n'est pas positif ! parce que j'ai pris un nombre hors de l'intervalle [-1;1] ?!(intervalle où le signe de x²-1 est négatif).

>erwan 16:17
Comment traduire, graphiquement, | x² - 1 | = m ?
Penses à des intersections de courbes...
Philoux
Je propose :
_ Si m = 0, alors l'équation |x²-1| = m a deux solutions : -1 et 1.
_ Si m = 1, alors l'équation |x²-1| = m a trois solutions distinctes.
_ Si m ]1;+
]1;+[, alors l'équation |x²-1| = m a deux solutions distinctes.

>> Erwan 
philoux étant déconnecté, je me permet de posé une question à sa place :
Et si m  ] 0 ; 1 [ ?
] 0 ; 1 [ ?
@+ sur l'
> Nightmare :
d'après la défnition de la valeur absolue j'en conclus ceci :
|x²-1| = x²-1 si x  0
0
|x²-1| = -(x²-1) si x  0
0
Cependant, avec x = -2, çà ne fonctionne pas 
> Lyonnais :
Si m appartient à ]0;1[, alors l'équation |x²-1| = m a quatre solutions distinctes 
> Philoux :
Pour le signe, on utilise les intervalles sur lesquels f est défnie ?
Bon Erwan on va reprendre.
Tu as dit que x²-1 était positif sur ]-oo;-1]U[1;+oo[ et négatif sur [-1;1]
Or on sait que |A| où A est une expression quelconque vaut A si A est positive et -A si A est négative.
On en déduit que |x²-1| vaut x²-1 est positive et 1-x² si elle est négative.
Mais on sait aussi que x²-1 est positive si x appartient à ]-oo;-1]U[1;+oo[ et négative si x appartient à [-1;1]
On en déduit que |x²-1| vaut x²-1 si x appartient à ]-oo;-1]U[1;+oo[ et 1-x² si x appartient à [-1;1]
c'est à dire :
Tu as compris ?

Jord
NM :
On en déduit que |x²-1| vaut x²-1 est positive et 1-x² si elle est négative.
"elle", c'est "x²-1" ?!
je continue à réfléchir sur ce que tu as dit...
Re 
Déja je voulait dire :
On en déduit que |x²-1| vaut x²-1 si x²-1 est positive et 1-x² si elle est négative.
oui , "elle" c'est l'expression x²-1

Jord
NM : Je t'embête encore un peu 
"Or on sait que |A| où A est une expression quelconque vaut A si A est positive et -A si A est négative".
> c'est : positive ou égale...et négative ou égale ?! (car si je remplace "-1" dans "x²-1" : j'obtiens 0 soit |0|=0, d'après la définition)
Je comprends mieux !
J'emploie positif pour positif ou égal (et strictement positif pour positif et non nul)
Mais ici ça ne change rien car la fonction est continue en 0

Jord
Pardon je voulais dire continue en -1 et 1
On pourrait écrire aussi :
ou encore :
ou bien :
C'est à la même chose dans tout les cas car en -1 et en 1 , 1-x²=x²-1=0

Jord

 |x²-1|
|x²-1|


