Inscription / Connexion Nouveau Sujet
Simple calcul.
Hello,
Comment peut-on passer de :
h(x) = 2x² - x
x
à
h(x) = 2x²  ( 1 - (1/(2x
( 1 - (1/(2x x)) )
x)) )
?!
(Dans l'optique d'étudier sa limite en +infini) 
Merci !
Erwan
en mettant 2x² en facteur et en se souvenant que x=(rac(x)).(rac(x)) pour x>0 puisque tu cherches la limite en +oo
Philoux
>erwan
ici, tu aurais pu ne mettre que x en facteur si c'est plus simple pour toi
La méthode, pour les études à l'oo de ce type de fctions, est de mettre le terme de + haut d° en facteur.
Philoux
Pourquoi "la limite de (sin x)/x, quand x tend vers 0, est égale à 1 ?

Re
As-tu vu les DL ?
sin x = x - x3/3 + o(x3)
Sinon, je crois (à faire confirmer/infirmer par plus compétents) que c'est un résultat qui vous est demandé de connaître en 1° sans qu'il vous soit possible, à votre niveau, de le démontrer.
A confirmer si je ne dis pas de bêtises...
Philoux
>NM
mais après ?
Je pensais au théorème des gendarmes en encadrant par des fctions polynomes du développement limité ?
Philoux
Merci philoux...le livre dit :
Comme d'après le cours, limite de (sin x)/x, quand x tend vers 0, égale à 1..
lol mais en fait je ne trouve pas où c'est marqué dans le cours alors je vous demandais 
comme tu le dis, çà n'a pas l'air d'être démontré...
Autrement , sur [0;pi/2] on a :
donc :
c'est à dire :
Or ,
donc d'aprés le théorème des gendarmes :
Et ainsi en prenant l'inverse :

Jord
>Nightmare :
On la trouve ta démonstration dans le livre "interro des lycées" chapitre 1 ?
NM
C'est sensé être connu sin(x) < x < tan(x) pour 0,pi/2 ?
Philoux
Non , je ne crois pas Erwan.
Pour ce qui est de l'encadrement magique que j'ai trouvé :
Il découle de :
Ensuite il suffit d'intégrer entre 0 et x

Jord
> Nightmare :
"intégrer entre 0 et x" ?
merci (pour les démonstrations  )
)
sinon on peut pas utiliser "la règle de l'hospital" ?! :
la dérivée de sin x : cos x
la dérivée de x : 1
Donc lim de cos 0, lorsque x tend vers 0, est égale à 1.
Merci

>erwan
La règle de l'hospital ne s'applique, sauf erreur, que pour la limite à l'infini.
N'oublions pas la blague favorite des profs de maths :
"La règle de L'Hospital? A n'utiliser qu'en cas d'urgence!".
Philoux
ok lol.
Philoux peux tu juste m'expliquer, comment Nightmare est passé du taux d'accroissement au nombre dérivé "sin'(0)" ? (cf post 14:56)^^
Merci beaucoup en tout cas.

La règle de l'hospital ne s'applique, sauf erreur, que pour la limite à l'infini.
Non non, ca s'applique également au cas 0/0.
>erwan
C'est la définition du nombre dérivée :
Soit I un intervalle ouvert, et x0 un point de I. On dit que f admet une dérivée à droite en x0 si l'accroissement :
( f(x) - f(x0) ) / ( x - x0 )
admet une limite quand x tend vers x0 par valeur supérieure (en restant plus grand que x0). Cette limite est alors notée f'd(x0).
De même, on dit que f admet une dérivée à gauche en x0 si le même accroissement admet une limite quand x tend vers x0 par valeurs inférieures (en restant plus petit que x0). On note f'g(x0) la dérivée à gauche.
Si f est dérivable à droite (resp. à gauche) en x0, on dit que la courbe représentative de f admet une demi-tangente à droite ou à gauche) au point (x0,f(x0)).
regardes ici : ![]() Cours sur les dérivées et la dérivation
Cours sur les dérivées et la dérivation
Philoux
Oui otto (salut) 16:19, tu as raison j'ai lu trop vite.
Pourquoi n'est pas enseigné en pré-bac ?
Philoux;
Philoux :
Ton post de 16:20 s'illustre t-il par un schéma 


Merci bien pour vos aides..j'ai deja pas mal appris en cette journée du 12 juillet 
>erwan
Ton post de 16:20 s'illustre t-il par un schéma
effectivement, ci-dessous :
Philoux
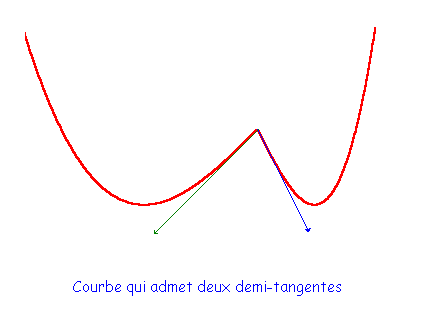
ok. je complète ton explication avec une explication de bouquin.


Ok erwan
Tu en as un exemple avec, par exemple :
y = f(x) = |x²-1| aux points d'abscisses -1 et +1
As-tu vu les valeurs absolues ?
Si oui, quelles sont les pentes des tangentes aux points A(-1,0) et B(1,0) ?
Philoux
on otient le nombre dérivé par le taux d'acroissement soit f'(a) qui n'est autre que le coefficient directeur de la tangente...
euh pour les valeurs absolues je les aies vu..mais dans une fonction çà m'embête un peu.
C'est un moyen simple pour générer des points anguleux et illustrer des 1/2 tangentes.
Exprimes f(x) sans valeurs absolues en définissant des intervalles...
Philoux
Si c'est trop difficile, passes à autre chose.
Re bonjour à tous
H_aldnoer> Attention , il manque la limite 
Philoux> On utilise l'inégalité des accroissements finis :
Si f et g sont dérivables sur [a;b] et telles que alors :
Donc ici , on peut écrire :
c'est à dire :
Autrement , le point qui est représenté par ton graphique est un point anguleux (deux demi-tangentes)

Jord
>NM
pas de soucis
mais les valeurs absolues semblent effrayer erwan.
Aurais-tu un ex. de fonction (simple) possédant un point anguleux non introduit par des valeurs absolues ?
Philoux
> Nightmare :
j'avais un peu de mal, mais là en parlant d'intégrales çà devient du chinois (pour l'instant) lol!
Philoux : tu veux dire prendre x 1 ou x
1 ou x 1 ?
1 ?

>erwan
Pour faire "disparaître" une VA, tu dois connaître le signe de l'élement entre les | |
Ainsi |g(x)|=g(x) si g(x)>=0
et
|g(x)|=-g(x) si g(x)<=0
donc les frontières sur x ne sont pas que x=1...
Philoux
son signe est positif sur:
]-;-1[U]1;+
[...
et négatif à l'intérieur des racines ?!
erwan 18:08 oui c'est bon
Je te laisse avec NM et sa fonction définie par intervalle.
Tu peux éventuellement continuer celle-ci
Bon courage
Philoux
Nightmare : autant prendre :
Au fait, le "mapsto" de TeX, il est où ???

Oui N_comme_Nul mais ça revient à la valeur absolue , chose qui ne plait pas à Erwan 
Je ne sais pas, il n'est pas integré au serveur je pense.

Jord
Salut Nightmare
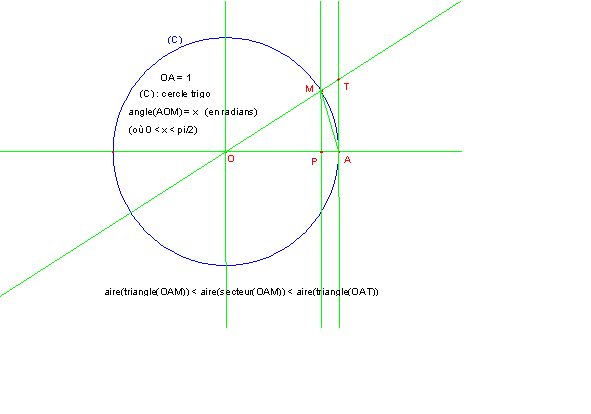
Pour montrer :
sin(x) <= x <= tan(x) lorsque x est compris entre 0 et pi/2 , il ya plus simple :
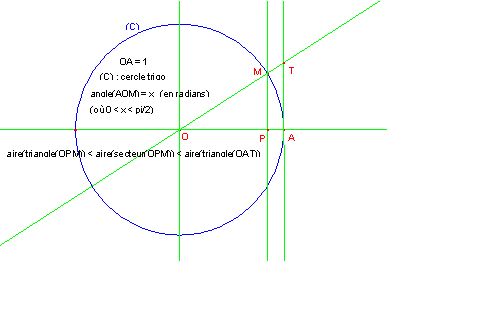
Erratum :
lire aire(secteur(OAM)) au lieu de aire(secteur(OPM))
jean-émile
Ce serait alors une suggestion à faire ça pour l'amélioration du site. 
Erratum 2
lire
aire(triangle(OAM)) <= aire(secteur(OAM)) <= aire(triangle(OAT))
jean-émile
je sais que :
|x| = x si x 0
0
|x| = -x si x 0
0
Sinon je vais plutôt m'atteler au cours du nombre dérivé et tangente...