Bonjour,
je ne comprend pas ta question.

bonjour Justin

Charles Hermite a démontré qu'elles sont résolubles à l'aide des fonctions elliptiques

sinon, la méthode de Sotta ( imaginée et mise au point par Bernard Sotta ) permet de résoudre certaines équations de degré supérieur ou égal à 4 si les coefficients de ces équations vérifient certaines conditions.

lis ici :


Par exemple, pour l'équation :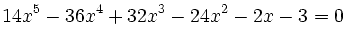

la méthode de Sotta permet de trouver les 5 racines :



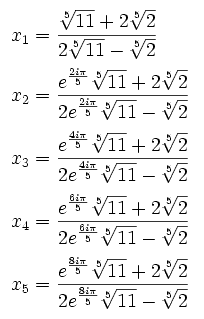
Bon courage !

Bonsoir

Maple ne donne pas de solution(s) exacte(s) donc...

http://fr.wikipedia.org/wiki/équation_quintique

maple ne donne même pas l'expression de la réelle, x1 ?

Bonjour Justin

La théorie de Galois dit seulement que pour une équation polynômiale de degré supérieu ou égal à 5 il n'y a aucune formule contenant des radicaux qui donne les solutions dans tous les cas. (Au contraire de l'équation du second degré pour laquelle on a bien la forrmule que l'on apprend au lycée). ceci n'exclut pas que l'on sache résoudre certaines équations. Pour une équation donnée, on peut toujours faire un calcul approché, ou même trouver des expressions avec des radicaux, mais pas de formule générale!

Merci a tous d'avoir repondu.

En fait, je me demandais a quoi pouvait ressembler une solution non exprimable seulement avec des radicaux.

Bonjour Justin,

Il y a beaucoup d'expressions mathématiques qui ne s'exprimment pas avec des radicaux.
Par exemple : sin(pi/7)
Alors si tu demandais :
"A quoi peut bien ressembler le sinus de (pi/7) qui n'est pas exprimable seulement avec des radicaux ? "
attends-toi à une réponse du genre :
" il resemble à sin(pi/7) et mieux encore, il est égal à la valeur de cette fonction".
Maintenant, dans un cas de solution générale de l'équation du cinquième degré, tu posais la question :
"A quoi pouvait ressembler une solution non exprimable seulement avec des radicaux ? "
Alors, on te répond de la même façon :
"Cela resemmble à une formule assez compliquée qui comporte des fonctions Theta de Jacobi et mieux encore, c'est exactement cette formule compliquée".
Quelle différence entre la fonction sin (qui est une fonction sinusoidale) et la fonction theta (qui est une fonction elliptique) ?
Disons que la première est plus couramment employée que la seconde !

"La théorie de Galois dit seulement que pour une équation polynômiale de degré supérieu ou égal à 5 il n'y a aucune formule contenant des radicaux qui donne les solutions dans tous les cas"



je suis pas un spécialiste de la question, mais j'avait cru comprendre que c'etait abel qui avait prouvé que l'équation géneral de degré 5 n'est pas soluble par radicaux, et que la théorie Galois permetait effectivement de savoir qu'elle etait les equations soluble par radicaux, donc ce que dit Justin est plausible.... enfin j'ai peut-etre mal compris

La méthode de Sotta ne marche pas pour l'équation car la résolvante de Sotta est nulle. Cependant on peut se faire une idée de la « tête » des solutions en regardant les radicaux de Bring.

Le radical de Bring est une fonction donnant la solution de l'équation particulière



et elle est analytique en . On la définit par une série entière. Voir la page pour la définition complète. Sur cette page, il est aussi expliqué comment se ramener à l'équation centrale .

Dans le cas de l'équation de Justin, les solutions sont
, , , , et .

En réponse à Ksilver :

le théorie de Galois dit simplement que, comme l'équation est de degré cinq, il n'existe pas de méthode générale pour en trouver les racines. C'est à dire pas de méthode que l'on pourrait appliquer pour toutes les équations de degré cinq. En effet l'équation est de degré cinq et est soluble par radicaux ! Puisque les solutions sont les pour .

Il existe, comme l'a remarqué mikayaou, certaines équations de degré supérieur à cinq pouvant se résoudre par radicaux. La méthode de Sotta est un exemple donnant les conditions de résolubilité par radicaux et les solutions. La théorie de Galois permet aussi de dire si l'équation est résoluble par radicaux mais ne donne pas la méthode de calcul des racines explicitement.

Le message de Justin était en fait ambigu, car on pouvait comprendre qu'il avait déjà analysé cette équation ou qu'il interprétait mal le résultat le plus marquant de la théorie de Galois.

Bonjour Hardy Potter, et bienvenue sur l'