Inscription / Connexion Nouveau Sujet
Spé maths : division euclidienne
Bonjour à tous, voila j'ai un exercice sur les divisions euclidienne en spé maths à faire pour la rentrée. J'ai réussi a faire la 1ère mais la 2ème je n'arrive pas, c'est pour cela que je suis venu ici.
Voici l'énoncé:
On sait que 1 000 000 000 011 = 111 111 111 111*9+12
1) Donner le quotient et le reste de la division euclidienne de 1 000 000 000 011 par 111 111 111 111.
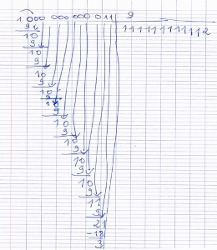
2) Donner le quotient et le reste de la division euclidienne de 1 000 000 000 011 par 9.
Mes réponses:
1) Le quotient est 9 et le reste est 11.
En 1 étape j'ai réussi à la faire elle est plutôt simple.
2) Pour celle ci je bloque.
Sur internet j'ai vu que le quotient est 2 147 483 647.
Mais en faisant la division euclidienne je n'arrive pas à trouver le reste qui devrait être 3.
Si je donne la réponse sans faire la division euclidienne ce n'est pas bon et sa ne sert a rien je pense...
Si vous pouvez m'aider à réaliser cette division euclidienne en mettant toutes les étapes ce serait TRES GENTIL de votre part.
Je vous remercie d'avance.
Bonjour,
Le résultat que tu as trouvé sur internet n'est pas juste, car 2 147 483 647*9+3
1 000 000 000 011. C'est quoi le site où tu as trouvé ça?
C'est sur ce site la que j'ai trouvé ce résultat : http://www.dcode.fr/division-euclidienne-entiere
Je te remercie beaucoup, ne t'en fait pas je me débrouillerais pour lire 
*
Merci encore 
J'ai un problème à résoudre, je l'ai résolu mais sans utiliser de méthode mathématiques ou scientifique, j'ai essayé les chiffres jusqu'à 50 mais il doit bien y avoir une méthode mais je la trouve pas. Pouvez vous m'aider sans me faire le travail.
L'énoncé:
Déterminer tous les couples d'entiers (x;y) tels que x²=y²+23
J'ai trouvé le couple (12;11) mais pour justifier je n'ai rien donc si pouvez m'aider à trouver une méthode ce serait utile pour trouver les autres couples.
Je vous remercie.
x2 - y2 = 23 <==> (x - y)(x + y) = 23
or les seuls diviseurs de 23 sont -23, -1, 1 et 23
donc
x - y = -23 et x + y = -1
ou
x - y = -1 et x + y = -23
ou
....
et on a donc quatre système à résoudre ...
Ou x-y= 23 et x+y= 1
Ou x-y= 1 et x+y= 23
4 systeme a resoudre:
1) x-y= -23 et x+y= -1
2) x-y= -1 et x+y= -23
3) x-y= 23 et x+y= 1
4) x-y= 1 et x+y= 23
J'ai pas assez de donnes pour resoudre ces systemes, j'ai 2 inconnu.
Sa donerais par exemple pour la 1) ceci :
x= -23+y et y= x+23 ?? Sa me donne rien de concret sa....
Bonjour,
111...11
Si l'on recherche l'origine possible de l'énoncé,
on peut revenir à la relation suivante:
Soit un nombre composé de n chiffres 1,
Annuler
connectez vous