Inscription / Connexion Nouveau Sujet
Statiques
Bonjour chers tous s'il vous plaît quelqu'un pourra bien m'accorder un peu de son temps parce je suis coincé sur exercice de statistiques là depuis maintenant 3 jours
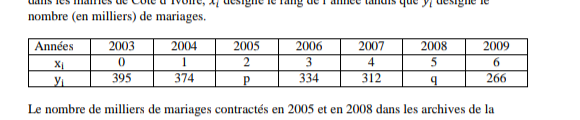
Le tableau suivant indique pour chaque année, le nombre de milliers de mariages contractés dans les mairies de Côte d'Ivoire, 𝑥𝑖 désigne le rang de l'année tandis que 𝑦𝑖 désigne le nombre (en milliers) de mariages.
Le nombre de milliers de mariages contractés en 2005 et en 2008 dans les archives de la direction générale des statistiques ont été égarées. Cependant, ces valeurs avaient permis par La méthode des moindres carrées d'obtenir la droite de régression de 𝑦 𝑒𝑛 𝑥 dont l'équation
réduite est la suivante : (𝐷): 𝑦 = −22𝑥 + 397.
1. On suppose que la relation entre 𝑥 𝑒𝑡 𝑦 traduire par la droite (D) reste encore valable pour
les années à venir :
a) A combien peut-on estimer le nombre de mariage en côte d'Ivoire au cours de l'année 2020 ?
b) A partir de quelle année l'on assistera à deux fois moins de mariages qu'en 2009 ?
2. a) Calculer la moyenne X et la variance V(X) de x.
b) Vérifier que la moyenne de y est
Y=(1681+𝑝+𝑞)/7
c) Démontrer : 𝐶𝑜𝑣(𝑥, 𝑦) =(2𝑞−𝑝−823)/
7
3. Déterminer les valeurs de p et de q.
J'ai fais la première question 1-a) et j'ai eu y=23 car en 2020, x=17 et j'ai remplacé dans l'équation donné d'où en il aura 23.000 mariages
Bonjour
Question 1 d'accord
question 1 b) équation à résoudre, vous connaissez y on vous demande x
problème inverse de a)
d'où
Quel problème avec les moyennes ?
Bonjour
Question 1 d'accord
question 1 b) équation à résoudre, vous connaissez y on vous demande x
problème inverse de a)
Quel problème avec les moyennes ?
[J'ai fais ça mais je vous que c'est pas logique.
Vu la question je le suis dis que j'allais divisé le y de 2009 par 2 et remplacer cette nouvelle valeur dans l'équation]
En divisant la valeur de y par 2 en remplaçant dans l'équation de y je trouve x=12 d'où c'est l'année correspond à 2015
Non, sauf si au numérateur, vous écrivez 133-397.
On ne peut avoir une réponse négative
Mais et si je me réfère à l'équation y=-22x+397
Et nous savons que
a=(Cov(X;Y)/V(X))
Mais aussi le hic est que nous deux inconnues
Quel est le problème ? Cette relation servira pour déterminer p et q
Calculez la covariance en utilisant la définition
Quel est le problème ? Cette relation servira pour déterminer p et q
Calculez la covariance en utilisant la définition
Non, il n'y en a qu'une qui s'annule
puis, on effectue la somme pour trouver
et par suite, ce qui est demandé.
Non, il n'y en a qu'une qui s'annule
puis, on effectue la somme pour trouver
et par suite, ce qui est demandé.
Après sa je vais poser une égalité pour l'équation 2p-q= 823
Ce n'est pas utile de recopier le message précédent. Cela alourdit pour rien.
Il vous reste à déterminer p et q.
Vous aviez dit où
est le coefficient directeur de la droite d'ajustement.
première équation
On sait aussi que le point moyen appartient à la droite de régression d'où seconde équation


