Inscription / Connexion Nouveau Sujet
statistiques
Bonsoir,
Problème avec un exercice de statistiquesvoici l'énoncé:
le gérant d'un hypermarché disposant d'un potentiel maximum de 16 caisses enregistreuses, a fait réaliser une étude statistique sur le tps moyen d'attente (en min) d'un client a la caisse.
xi = 4/5/6/7/8/9/10/11/12/13
yi = 12.25/12/11.5/11.75/10/10/9.75/9/8.25/8
xi = nombre de caisses ouvertes
yi = tps moyen d'attente correspondant
Rq:12.25min = 12min et 15sec
On suppose qu'il y a tjs au moins 4 caisses ouvertes.
1) construire dans un repere orthogonal, le nuage de points associé à ce tableau statistique.(c'est fait)
2)Calculer les coordonnées du point moyen G de la série précédente. Et placer G. (c'est fait)
3)Calculer les coordonnées du point moyen G1associé aux 5 premiers points du tableau, puis celle du point G2 associé aux 5 autres points. Placer G1 et G2 et tracer la droite d'ajustement (G1G2).(c'est fait)
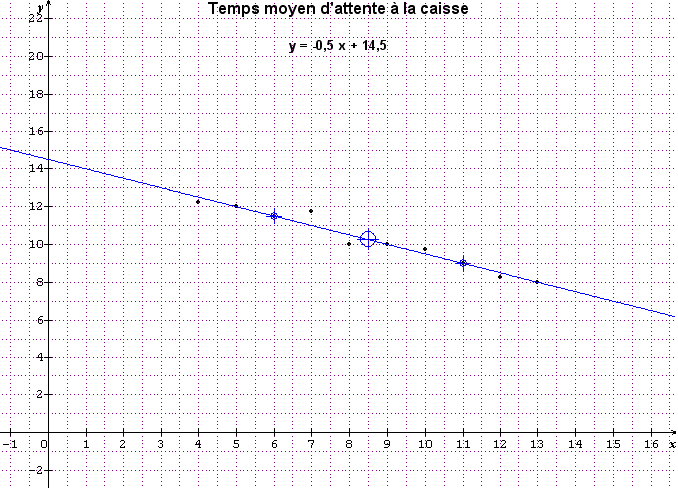
4)Déterminer une équation de la droite d'ajustement (G1G2)
5)En utilisant la droite d'ajustement (G1G2), déterminer le temps moyen d'attente d'un client à la caisse lorsque 16 caisses sont ouvertes. (c'est fait)
6)D'après l'approximation affine précédente, si l'on veut qu'un client n'attende pas plus de 7 min en moyenne, combien de caisse doit-on ouvrir? (c'est fait)
en somme il me reste la question 4) a faire...
voila mes résultats des autres questions pouvez-vous me dire si ils sont exactes!!
merci
Oups j'avais oublié de poster mes réponses!!
2)G(8.5;10.25)
3)G1(6;11.5) et G2(11;9)
5) 6min et 30sec
6) 15 caisses


 statistiques en Bts
statistiques en Bts