Inscription / Connexion Nouveau Sujet
Statistiques à 2 variables
Bonjour à tous , je souhaiterai de l'aide pour la fin d'un exercice, donc si quelqu'un pourrait m'aider svp .
J'ai calculé les coordonnées du point G qui sont : G(5.5;2.66)
J'ai fait de même pour G1 et G2 G1(3;1.75) G2(8;3.56)
J'ai aussi determiner la droite (G1G2) sous la forme y=mt+p
m= ya-yb/xa-xb
m=2.83-1.74/6-3
m= 0.36
y=mt+p
yG1=0.36*tG1+p
1.75=0.36*3+p
1.75-0.36*3=p
p=0.67 Je pense que tout mes calculs sont juste mais apres cette question on me dit en admettant que cette droite donne une approximation satisfaisante de la variation de y en fonction de t, montrer que N(t)= 1500(1-1/0.36+0.68)
Non seulement je ne sais pas comment montrer et je trouve p=0.67 et dans la formule on retrouve 0.68 je me demande si il n'y a donc pas une erreur dans mes calculs.
Merci de vos reponses.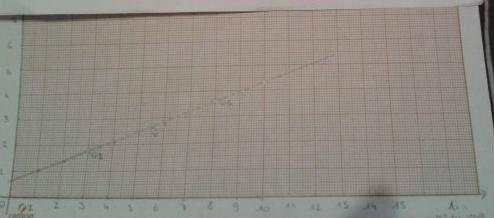
* Océane > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum  *
*
bonsoir
il faudrait donner le texte et non un scan peu lisible cependant il me semble apercevoir que m et p doivent être arrondies au millième
ce que vous n'avez pas fait L'erreur vient sans doute de là
on vous dit
et vous connaissez y en fonction de t
il suffit donc de tirer N(t) de cette relation
Je n'ai recopier que l'essentiel mis à part le tableau si il faut je reocpie tout, Recopier et completer le tableau ci dessous en arrondissant les valeurs à 10^-2 près.
je ne comprends pas vos calculs pour l'équation de la droite (GG
ce doit être une question d'arrondi
Comment ça ? Je trouve 0.36 aussi , avec mes calculs du tableau, ce qui me pose probleme c'est pour p.
Ou trouvez vous les valeurs 3.56-1.75 / 8-5
Ah d'accord merci , donc m= 3.56-1.75/8-5 = 0.60 ?
J'etais persuadé d'avoir juste vu que je trouvais 0.36 comme la question suivante
je redonne le calcul avec les coordonnées de Get G
donc on trouve bien 0.36 puisque j'avais écrit 5 au lieu de 3
mais la réponse était correcte
pour p on a bien 0.67
Merci donc c'est juste mais je pensais qu'il fallait trouver 0.68 comme le montre la question d'apres.
Et donc pour cette question pourriez vous m"eclairez pour la demarche je ne sais pas trop comment proceder.
Bonjour
je vous avais donné une indication dans le message de 21h 10
vous avez
en prenant la valeur donnée
à partir de cette relation , il suffit de tirer
N(t)= 1500(1-1/0.36t+0.68)
0.36t+0.68=1500/1500-N(t)
Je ne sais vraiment pas comment faire pour tirer N(t)
Parce que apres cette question il me demande d'estimer à partir de combien de jours donc (ti) l'operateur peut esperer convaincre au moins 90% des salariés de cette entreprise.
Car un operateur propose au salariés de tester un type de portable et il dispose de 10 jours (ti) pour les convaincre de changer.
Donc pour savoir a partir de combien de jours l'operateur peut concainvre 90% il faut remplacer les 90% dans la formule ? Mais ou ? Je suis un peu perdu la...
Bonsoir
produit en croix
division par un même nombre non nul
on isole N(t)
à vous de terminer
que signifie N(t) ?
bonsoir
vous n'avez pas terminé le calcul
vous n'avez pas répondu à la question vous n'avez pas donné le texte et je ne peux deviner
Le texte est un operateur desireux de gagner des parts de marché propose aux salariés d'une entreprise de tester un nouveau type de telephone portable. Pour cela il dispose d'au moins 10 jours pour convaincre les salariés de changer de telephone. Le tableau ci dessous indique les resultats observés
Ti= numero du jour : 1 2 3 4 5 6 7 8 9 10
Ni nombre salariés concaincu: 40 420 640 790 900 970 1040 1080 1110 1150
le nuage de points associé n'est pas allongé et ne permet pas un ajustement affine on pose
yi= 1500/1500-Ni
Ti : 1 2 3 4 5 6 7 8 9 10
yi :1.03 1.39 1.74 2.11 2.50 2.83 3.26 3.57 3.85 4.29
construire le graphique determiner les coordonnées de G1 G2 en prenant les 5 premiers points et les 5 derniers.
placer G1 et G2 et tracer la droite (G1G2)
Determiner une equation de la droite (G1G2) sous la forme y=mt+p on donnera les valeurs arrondies de m et de p à 10^-2 près.
En admettant que cette droite donne une approximation satisfaisante de la variation de y en fonction de t, montrer que N(t)= 1500(1-1/0.36t+0.68)
Puis estimer à partir de combien de jours l'operateur peut esperer convaincre au moins 90% des salariés de cette entreprise.
Bonsoir
merci pour le texte mais il manque une donnée combien de salariés dans l'entreprise ?
vous prenez 90% de ce nombre pour simplifier je vais l'appeler A et vous résolvez l'inéquation en t
j'ai refait les calculs , ils sont corrects
Bonsoir,
J'avais un autre exercice sur les probabilité avant ou il y avait 1500 salariés mais les des exercices sont independants mais effectivement il faut prendre les 1500 salariés surement.



