please

Bonjour elieval

Que voilà un exercice intéressant et important...

Regarde bien comment est "fabriqué", comment est obtenu, calculé, ce d²

Il calcule les écarts entre les fréquences qui sont observées (les f_c ou f_s ou f_a) et ce qui est attendu si la loi est celle à laquelle on pense. Si la répartition est uniforme alors les fréquences attendues valent toutes les trois 1/3

Donc il fait la somme de ces écarts. Mais pour que des écarts positifs (même très importants) ne soient pas annulés par des écarts négatifs (même très importants) il prend la précaution de commencer par élever au carré ces écarts, ces différences. D'où une somme de carrés des écarts (tu reconnais quelque chose qui ressemble à ce que tu fais quand tu calcules une variance).

Si les fréquences observées étaient miraculeusement égales à 1/3 alors les trois écarts seraient nuls de même que leurs carrés et donc que d²

Mais tu sais bien que le hasard de l'échantillonnage va faire fluctuer les fréquences observées même si la vérité du bassin de truites est que les fréquences réelles y sont égales.

D'où la simulation...

A l'ordinateur, il simule pour savoir quelles sont les valeurs de 400.d² que l'on peut obtenir quand on est sûr que la population de départ a bien des fréquences égales.

Le hasard fait que 539 fois sur 1 000 le 400.d² est compris entre 0 et 0,5
etc.

Même en partant d'une population dans laquelle les fréquences sont bien égales, le hasard peut faire que 400.d² soit compris entre 2,5 et 3 ; mais c'est quand même une proportion de cas très faible, un événement plutôt rare puisqu'il se produit seulement 12 fois sur 1 000
_______________________

Quelle est ton approximation du 9^ème décile de cette distribution ?
90 % des valeurs de 400.d² sont inférieures à ...
seulement 10 % des valeurs de 400.d² sont supérieures à ...

J'ai oublié de dire que ton calcul de probabilité à la fin de l'exercice est exact.

merci Coll
les stats, c'est presque pire que la géométrie dans l'espace
je n'avais pas compris que "prélèvement au hasard de 400 truites suivant la loi équirépartie" signifiait : "on prélèves 400 truites dans 1 bassin où les truites sont réparties en 3 catégories de même nombre"!
donc pour les quartiles j'ai calculé les ECC.
le 9ème quartile va correspondre à un effectif cumulé croissant de
la 900è valeur est la 4è valeur de la classe [1,5;2[ et donc vu qu'on me demande une réponse approchée à 0,5 près par défaut, je dirais que D₉=2
ce qui signifie que 90% des valeurs de d² sont comprises dans l'intervalle [0;2[ ?
si on m'avait demandé une valeur exacte du 9ème décile, comment fallait-il faire?
je sais que l'écart de l'intervalle [1,5;2[, dans lequel se trouve D₉ est de 0,5
le 9è décile est la 4è valeur de cet intervalle (896+4=900). MAis comment poursuivre?

Tu as Sine qua non je suppose...

Voici le polygone des fréquences cumulées croissantes qu'il dessine :



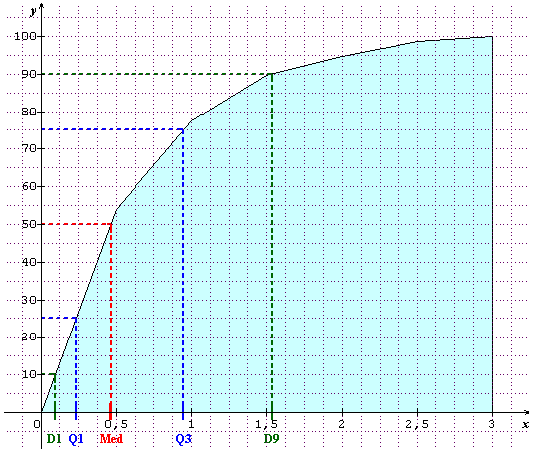
et voici le tableau correspondant :



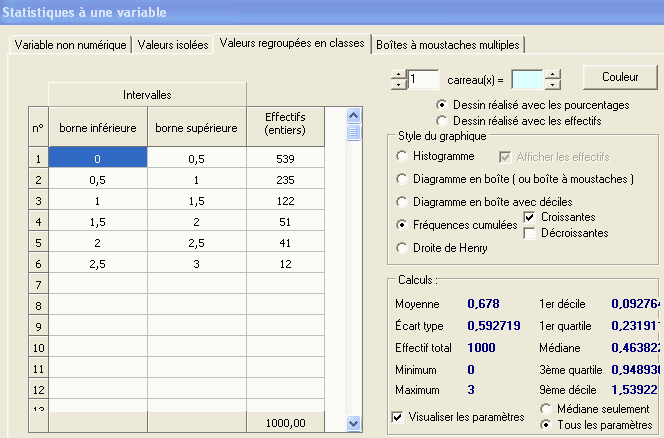
Le neuvième décile est beaucoup plus proche de 1,5 que de 2
jusque 1,5 tu as déjà un effectif cumulé croissant de 896 et il n'en manque que 4 qui seront vite obtenus dans l'intervalle [1,5 ; 2[ qui a un effectif de 51

Je n'ai pas vérifié mais je suppose que Sine qua non fait une interpollation linéaire entre les points (1,5 ; 896) et (2 ; 947) pour trouver l'antécédent de 900 et donc il propose 1,54 environ.

La valeur approchée à 0,5 près par défaut est donc 1,5
Elle suffit tout à fait pour la suite du raisonnement.

j'ai confondu par défaut et par excés! par excès on aurait pris 2!?
OUI j'ai sine qua non mais je n'en avais pas cet usage!
ma TI82 stat me donne aussi tout ça je suppose!

"en argumentant soigneusement la réponse dire si on peut affirmer avec 1 risque d'erreur inférieur de 10% que le bassin contient autant de truites de chaque variété."
il me reste encore cette question!

C'est l'un des raisonnements les plus utiles en statistiques et probabilité ; mais il n'est pas facile à bien saisir les premières fois où on le rencontre.

Plus les truites sont en proportions inégales et plus d² est élevé.
Donc on va se fixer une limite pour la valeur de d² trouvée lors du prélèvement.
Si le d² que l'on trouve est supérieur à cette limite on dira que les truites sont en proportions inégales ; si le d² est inférieur à cette limite on considérera que l'on n'a pas de raison de croire que les truites sont en proportions inégales et donc on admettra qu'elles sont en proportions égales.

A cause des hasards du prélèvement on peut se tromper dans la conclusion.
Croire qu'elles sont en proportions inégales alors qu'elles sont en proportions égales.
Admettre qu'elles sont en proportions égales alors qu'elles sont en proportions inégales.

Cela est le "risque" de se tromper en prenant une conclusion au vu du résultat d'un prélèvement.
_________________________

Ici, le pisciculteur peut donc tenir le raisonnement suivant :
si 400.d² dépasse le 9^ème décile (dépasse 1,5)
. ou bien je continue de croire que les truites sont en proportions égales et j'appuie ma décision sur un événement assez rare puisque la simulation a montré que ceci se passe dans moins de 10 % des cas
. ou bien je refuse de prendre cette décision à partir de cet événement rare et je conclus en conséquence que les truites sont en proportions inégales ; ceci avec un risque d'erreur qui est inférieur à 10 %

Ce n'est pas exactement la formulation de ton énoncé, mais je ne peux faire mieux...

ça commence à être plus clair!
ce que je ne comprends pas bien c'est comment interpréter le "avec un risque d'erreur inférieur à 10%!
c'est ça qui t'a amené à dire "si 400 d² dépasse le 9è décile" ?

Oui, la proportion des cas qui dépassent le 9^ème décile vaut 10 %

merci!
je retravaillerai ce ci plus tard! je suis dans les limites ce soir!

encore une question Coll
est ce que si la question avait été "en argumentant soigneusement la réponse dire si on peut affirmer avec 1 risque d'erreur inférieur de 20% que le bassin contient autant de truites de chaque variété" dans ce cas on aurait calculé Q₈ le 8ème décile?

Oui, si tu veux, bien que ce ne soit pas classique.

Pour "argumenter soigneusement" il faut un énoncé sans reproche, ce qui est loin d'être le cas ici.

. on n'affirme pas en statistiques ; on conclut, et cela avec un risque d'erreur.
. le risque d'erreur n'est ni "inférieur de 10 %" ni "inférieur de 20 %" mais "inférieur à 10 %" ou "inférieur à 20 %"
. mais le plus grave est que ce risque d'erreur est, évidemment, un risque de se tromper ; il n'y a pas de risque d'erreur si l'on a raison...
Or, si le bassin contient des truites en proportions égales et que l'on conclut que le bassin contient des truites en proportions égales... on ne se trompe pas !
On se trompe si on conclut que le bassin contient des truites en proportions égales alors que ce n'est pas le cas ; et pour calculer ce risque il faut pouvoir calculer la probabilité de trouver une valeur de 400d² 1,01 ; ce qui n'est pas le cas ici ; on n'a pas de données pour pouvoir le faire.

C'est seulement si on avait trouvé un 400d² 1,54 que l'on aurait pu conclure que le bassin ne contenait pas des truites en proportions égales et que cette conclusion aurait été prise alors avec un risque d'erreur inférieur à 10 %

Mais tout ceci est fort délicat et demande de bien y réfléchir...

rebonjour Coll!
j'ai vu qu'un sujet de ce type est tombé en amérique du nord : juin 2009.j'ai essayé de le faire(juin 2009) Bac ES - Amérique du Nord - Juin 2009
1 pépiniériste a planté 3 variétés de fleurs des violettes (179); des primevères (133) des marguerites(188) soit 500 fleurs.
calculer 500d²=(fv-1/3)²+(fp-1/3)²+(fm-1/3)²voici ce que j'ai trouvé.
peux-tu me dire si c'est correct? merci!
j'ai calculé 500d²observé=3,481.
Le pépiniériste opère sur ordionateur en simulant le comptage au hasard, de 500 fleurs suivant la loi équirépartie. Il répète 2000 fois l'opération et calcule à chaque fois la valeur de 500d².voici les résultats
[0;0,5[   [0,5;1[   [1;1,5[  [1,5;2[  [2;2,5[  [2,5;3[  [3;3,5[  [3,5;4[  [4;4,5[  [4,5;5[
163        439       458      350      231       161      80       47      37          34
163        602       1060     1410     1641      1802    1882    ...      
(la 3èligne correspond aux ECC (je ne suis pas allée jusqu'au bout)

J'ai calculé le 9èdécile 2000/10 .9=1800
et je dis que lorsque les fleurs sont réparties de façon égale (1/3),90% des valeurs de d² sont <3
or le pépiniériste a trouvé une valeir de d²=3,481
donc on ne peut pas affirmer,avec un risque < à 10%, que sa prairie contient autant de fleurs de chaque variété.
merci de me dire si c'est juste!