Inscription / Connexion Nouveau Sujet
Sudo(ku)-maths sur la dérivation
Bonjour tout le monde, mon prof de maths a fait dans l'originalité et nous a donné un dm sous forme de sudoku, j'aurais apprécié avoir un peu d'aide car je ne suis pas trés forte en dérivée!
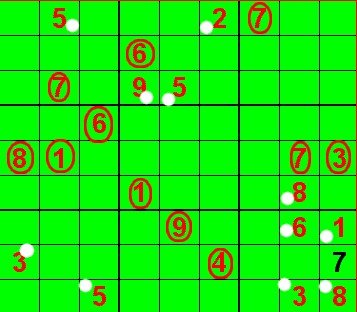
Rappel: La grille doit etre complétée avec tous les chiffres de 1 à 9,chacun devant être utilisé une seule fois dans chaque ligne, chaque colonne et chaque région (gd cube)
je vous joint donc la grille :
les fonctions utilisées :
(^= puissance)
=> On définit f par f(x) = x^3 + 2
=> On définit g par g(x) = (x²+1) (5x+2)
=> On définit h par h(x) = (x+2)/(x-1)
=> On définit k âr k(x) = (1/3)x^3-4x²+7x+1
=> On définit l par l(x) = (2x+1)²
=> On définit m par m(x) = x^5 + (1/2)x²-x
=> On définit b par b(x) = 6x+2
=> On définit d par d(x) = x² - 18x+2
=> On définit R par R(x) = Vx + x/2
=> Soit S une fonction vérifiant S'(x) = (x-1)(x-2)(x-3)(x-4)
=> Soit T la fonction vérifiant T(x) = 4x²+8x+7
=> On définie V par V (x) = 3/(2x+1)
Consignes à suivre:
1) Recopier la grille du "Sudo-maths"
2) Remplacer les énigmes par les chiffres correspondant (on écrira en ROUGE ces chiffres dans la grille). Vous justifirez les résultats obtenus..
3) Enfin, vous compléterez la grille comme un SUDOKU classique. Vous utiliserez pour cette question du bleu ou du noir afin de bien différencier les chiffres de la question 3 avec ceux de la question précédente.
Merci de bien vouloir m'aider ^^
Lety
Edit Kaiser : image insérée sur le serveur de l'
Bonjour,
Case en haut à gauche.
f(x) = x^3+2
On cherche f'(2) :
f'(x) = 3x²
f'(2) = 12.

Merci 
Estelle 
Merci de me répondre, et bien déjà j'aimerais savoir:
quand il dit "dérivée de la fonction f en 2", qu'est ce que cela veut dire exactement? quand x vaut 2?
sinon j'ai trouvé:
deuxieme case en partant de la gauche:
"dérivée de la fonction x²+5x en x=0" : 2x+5 = 2*0+5=5
la 6eme case en haut en partant de la gauche:
"g(0)" g(x)= (x²+1)(5x+2)=1*2=2
diamant952 >> "Dérivée de la fonction f en 2" <=> "Valeur de f'(2)".
Par contre je trouve 12 pour cette case (cf 10:03) 
Est-ce que tu peux aussi redonner ce qui est écrit dans la case en bas à gauche de la région du milieu de la colonne de droite ? (Celle où il y a le trombone  )
)
Estelle 
il y a un truc de bizare , car le resultat d'estelle est bon , mais 12 n'apparait pas dans les cases de sudoku 
où est l'erreur ?
sinon , pour la pente d'une parallele à la tangente de Ck au point d'abscice 0 .
Si une droite est parallele à une tengente , alors leur coefficient directeur est le même (pente)
ainsi tu dois trouver l'equation de la tangente pour en deduire sa pente .
utilises :
où "a" correspond au point d'abcsice .
non aucune erreur d'énoncé, je ne comprends pas :S
^pour la case ou il y a le trombonne c "nombre de solutions de l'équation f'(x)=5"
diamant592 >> Peux-tu vérifier l'expression que tu as donnée de f(x) ? L'erreur est sûrement là car pour la case du trombone, ça ne va pas non plus 
Estelle 
pourtant j'ai bien f(x)=x au cube + 2
Tiens je viens aider un pue
ou est el probleme??
Bon je vous mets les réponses que j'ai trouvé, merci de prendre le temps de me corriger de mes éventuelles erreurs 
=> Dérivée de la fonction x²+5x en x=0
2x+5 donc 2*0+5 = 5
=> g(0)
g(x)=(x²+1)(5x+2) = (0²+1) (5*0+2) = 1*2 = 2
=> Dérivée de la fonction 9x+3 en x=100
donc 9
=> g'(0)
g(x) = (x²+1) (5x+2)
u(x) = x²+1
u'(x)=2x
v(x)=5x+2
v'(x)=5
2x*(5x+2) + (x²+1)*5
10x² + 4x + 5x² + 5
15x²+4x+5 = 5 pour g'(0)
=> Nombre de solutions de l'équation f'(x)=5
f'(x)=3x²
3x²=5
3x²-5=0
 =0²-4*3*(-5)=60
=0²-4*3*(-5)=60
60>0 donc 2 solutions
=> Nombre dérivé de T en x=0
T(x)=4x²+8x+7
=4*2x+8
=8x+8=8
=>f(1)
f(x)=x^3+2
1+2=3
=>Taux de variation de la fonction b entre 1 et 1000
b(x)=6x+2
a=>0
a+h=>1000
b(a+h) => b(1000)=6*1000+2=6002
b(a) => b(1)=6*1+2=8
h= (a+h) - a = 1000-1 = 999
(6002-8)/999 = 5994/999 = 6
=> R'(1)
R(x) = Vx + x/2
R'(x) = 1/(2Vx) + x*1/2
=1/(2Vx)+1/2
=1/2 + 1/2 = 1
=> f'(1)
f'(x) = 3x²
f'(1) = 3 * 1 = 3
=> m'(1)
m(x) = x^5 + 1/2x² - x
5x^4 + 1/2 * 2x -1
=5+1-1=5
=>Image de 5/2 par la fonction h
h(x) = (x+2)/(x-1)
h(5/2) = (5/2 + 2)/(5/2-1)=9/3=3
=>Carré du nombre 2V2
(2V2)² = 4V4=4*2=8
Voila merci de votre aide et si vous pouvez me guider pour le reste ce serait gentil merci
J'ai mis un point blc là où je suis d'accord et où j'ai compris, et j'ai entouré en rouge là où j'aimerais que vous m'expliquiez si possible, merci pour votre aide
édit Océane : image placée sur le serveur de l' , merci d'en faire autant la prochaine fois
, merci d'en faire autant la prochaine fois 
k(0)=1
donc y=mx+1 (pour x=0, y=1 car le point est sur la tangente)
pour info, m=7 mais c'est sans intérêt ici!
Merci pour ton aide mais pour "posté par : garnouille
pour le "6" de la 2ème ligne, je ne suis pas d'accord, je trouve 2 car b'(x)=2"
ceci n'est pas possible car dans la même case il y a déjà le chiffre "2" ^^
Sinon Estelle si tu passes par là et si tu peux m'expliquer pour ceux qui restent ce serait sympas
j'vous remercie!
bisoux!
bonne journée
Bonjour Diamant. J'ai une solution pour ton Sudok' ...
J'ai seulement éliminé le (-6) contesté et je l'ai terminé hier. Si cela t'intéresse encore, je l'envoie ici, en entier, ou si tu veux en partie, ou encore ... rien du tout ?...
Tu me réponds ?...
jacqlouis, je veux bien, je te remercie! et si possible m'expliquer par la meme occasion, si tu n'as pas le tps pas grave j'éssaierais de chercher seule ou si estelle ou quelqu'un dautre veux bien...
enfin déjà merci pour toute l'aide apportée!
bonne soirée
pour le "6" de la 2ème ligne, je ne suis pas d'accord, je trouve 2 car b'(x)=2"
oups!

à force de faire des "aller et retours"..
On définit b par b(x) = 6x+2 donc b'(x)=6
OK pour ce "6"
Bonsoir Diamant.J'ai donc posé la question ici... car il y a quelques mois, j'avais envoyé une solution, et j'ai été blâmé de l'avoir fait (certaine se reconnaîtra...). Voici donc la solution que j'ai trouvée, en supprimant le (-6) qui ne collait pas... J'espère qu'elle est valable... sauf distraction comme certains disent...
1 5 8 3 4 2 7 9 6
9 4 3 6 7 1 8 5 2
2 7 6 9 5 8 3 1 4
6 3 7 8 2 9 1 4 5
8 1 9 4 6 5 2 7 3
5 2 4 1 3 7 6 8 9
4 8 2 7 9 3 5 6 1
3 6 1 5 8 4 9 2 7
7 9 5 2 1 6 4 3 8 Bonne chance avec cette grille ..
si possible m'expliquer par la meme occasion
c'est très long de tout expliquer... mais pose des questions précises, on te répondra!
on en est donc à deux erreurs d'énoncé : 1ère case et 4ème ligne 3ème case...
le "2" de la 3ème ligne 1ère case
g(x)=(x+1)²(5x+2)
tangentes horizontales pour g'(x)=0
g(x)=5x3+12x²+9x+2
on dérive et on résout g'(x)=0
on trouve deux solutions
le "2" de la 2ème ligne dernière case :
tangente horizontale pour Cf
f'(x)=0
3x²=0
x=0
valeur de f : f(0)=2
jacqlouis,
petit soucis pour la case du trombonne
6 solutions pour f'(x)=5
ça fait beaucoup pour une équation de degré 2 
Pour moi, la case " trombonne " n'était pas à deviner , c'est soit une blague, soit une sorte de case inconnue: il n'y avait pas à essayer de savoir...
Comme il n'y a pas à chercher le nombre d'erreurs (s'il y en a?) commises par l'auteur de cette grille !... Cela arrive qu'il y ait des erreurs dans un énoncé, on n'en fait pas tout un plat !
merci de votre aide!! je vais essayer de comprendre mieux tout ça toute seule et si j'ai des questions je me tournerais vers vous
merci pour votre aide
bonne fin de journée
. Bonjour . Pour comprendre tout cela (je ne parle plus des cases renseignées par les dérivées...), il faut que tu connaisses le mode de fonctionnement des Sudok's . Sinon, les explications risquent d'être longues !...
Je te rappelle que j'ai terminé la grille , en faisant quelques impasses ... (celle du 6 , n°3 de la ligne 4; et case " trombone"). Si ces impasses étaient erronées, la grille entière serait à refaire :...
merci pour la précision!
garnouille est ce que tu pourrais m'expliquer :
pour
le "2" de la 3ème ligne 1ère case tu dis que
g(x)=(x+1)²(5x+2)
tangentes horizontales pour g'(x)=0
g(x)=5x3+12x²+9x+2
on dérive et on résout g'(x)=0
on trouve deux solutions
or g(x) = (x²+1)(5x+2)
et quand je développe ça me donne ceci :
5x^3+2x²+5x+2
soit g'(x)=5*3x²+2*2x+5
=15x²+4x+5
soit 15x²+4x+5=0
 = 4²-4*15*5=-284
= 4²-4*15*5=-284
donc le discriminant est négatif ce qui voudrait dire qu'il n'y a pas de solution :S
je ne comprends pas trop
le "2" de la 3ème ligne 1ère case :
g(x)=(x+1)²(5x+2)
g(x)=(x²2x+1)(5x+2)
g(x)=5x3+2x²+10x²+4x+5x+2
g(x)=5x3+12x²+9x+2
tangentes horizontales pour g'(x)=0
on dérive et on résout g'(x)=0
on trouve deux solutions
pour le reste, je trouve ce sujet intéressant mais il faudrait s'entendre sur l'énoncé et donc les cases à trouver doivent être les mêmes pour tous !
si je traque l'erreur d'énoncé, c'est dans ce seul but!
et je n'attaque en rien le concepteur du sujet qui apportera certainement des éclaircissements!
et donc encore une erreur...
puisque c'est g(x)=(x²+1)(5x+2)
donc les calculs de diamant sont corrects et la réponse serait 0
j'avais trouvé celà d'abord puis j'ai modifié l'énoncé sans même y faire attention pour que "ça marche"
trois erreurs éventuelles plus l'interprétation du trombonne,
on est vraiment dans le flou artistique...
moralité : sudoku impossible sans interprétations diverses et variées!!
dommage!
Non, pas dommage !...
Si tu veux vraiment le faire, prends les cases telles qu'elles figurent dans la grille d' Estelle (sauf le 6 de la 4ème ligne)... et tu verras ce que cela donne.
De toutes façons, je me demande si Diams nous donnera un corrigé ?...
dans ce cas, ce n'est plus du tout le même sujet!
mais après tout, pourquoi pas?
il suffit de savoir ce que l'on cherche!!
Bonsoir,
jacqlouis >>
Si tu veux vraiment le faire, prends les cases telles qu'elles figurent dans la grille d' Estelle (sauf le 6 de la 4ème ligne)... et tu verras ce que cela donne.
Je n'ai pas tout lu mais quel est le problème avec le "6 de la 4ème ligne" ?
Estelle

quel est le problème avec le "6 de la 4ème ligne"
v'(-1)=-6 et pas 6
On définit V par V (x) = 3/(2x+1) donc V'(x)=-6/(2x+1)² et c'est toujours négatif!
alors tu traduis, "valeur absolue du nombre dérivé"... pourquoi pas , mais c'est une interprétation!
Jacqlouis a supprimé le nombre... moi, je ne sais pas quoi faire!
en tous cas, nous sommes trois et nous avons trois réactions différentes!!

Personnelement, ça me paraît évident 
La valeur de ce nombre, c'est bien ce qu'il vaut, càd 6.
Et si on conserve ce 6, on en vient à conclure que la seule erreur d'énoncé est dans l'expression de f.
Estelle 


