Bonsoir

Que proposez-vous ? Quels sont vos problèmes ?

Bonjour :

Pour les question 1) , 2), 4)a), 4b) et 4c) je pense que ce que j'ai mis est juste est ce que vous pourriez juste me confirmer si c'est juste et les questions 3a), 3b) 5a), 5b) je n'arrive pas à les faire

voila

pour la questions 1) j'ai mis : Nombre N de tigres dans la réserve en 2020 : N = 0, 9 × 100 + 5 = 95

pour la question 2) j'ai mis u₀ = 100, comme 10 % de tigres meurent d'une années à l'autre, il en reste 90 %
auquel on rajoute 5, ce qui donne pour tout n ∈ N, u_n+1 = 0, 9_un + 5

pour la question 4a) ∀n ∈ N, v_n+1 = u_n+1 − 50 = 0, 9_un + 5 − 50 = 0, 9_un − 45 = 0, 9(un − 50) = 0, 9_vn
La suite (vn) est géométrique de raison q = 0, 9 et de 1er terme v₀ = u₀ − 50 = 50.

pour la question 4b) : v_n = v₀ qⁿ = 50(0, 9)ⁿ donc un = 50(0, 9)ⁿ + 50

pour la question 4c) : lim n→+∞ 0, 9
n = 0 car −1 < 0, 9 < 1, par produit et somme lim n→+∞
un = 50

voila

Bonjour

Vous n'avez pas mis ce que vous avez effectué  donc pas d'avis possible

Je ne vois pas pourquoi un raisonnement par récurrence





b) on a une suite décroissante  minorée par 50 donc elle converge

5  Je ne connais pas Python donc son écriture

while  u \geqslant 60

u=0,9u+5
n=n+1

print n

faites tourner cet algorithme


le nombre d'années qu'il faudra

si j'ai mis ce que j'ai mis comme réponse a 9h 47 vous ne voyez pas ?

pour la questions 1) j'ai mis : Nombre N de tigres dans la réserve en 2020 : N = 0, 9 × 100 + 5 = 95

pour la question 2) j'ai mis u0 = 100, comme 10 % de tigres meurent d'une années à l'autre, il en reste 90 %
auquel on rajoute 5, ce qui donne pour tout n ∈ N, un+1 = 0, 9un + 5

pour la question 4a) ∀n ∈ N, vn+1 = un+1 − 50 = 0, 9un + 5 − 50 = 0, 9un − 45 = 0, 9(un − 50) = 0, 9vn
La suite (vn) est géométrique de raison q = 0, 9 et de 1er terme v0 = u0 − 50 = 50.

pour la question 4b) : vn = v0 qn = 50(0, 9)n donc un = 50(0, 9)n + 50

pour la question 4c) : lim n→+∞ 0, 9
n = 0 car −1 < 0, 9 < 1, par produit et somme lim n→+∞
un = 50

voila ce que j'ai mis aux questions

1 u=100
2 n=0
3 while u<60
4             u=0,9u +5
5             n=n+1
6 print (n)

sa donne ça pour l'algorithme  ducout ? et je ne sais pas faire tourner l'algorithme

J'étais en train de vous répondre donc je n'avais pas vu vos réponses
Attention à l'écriture  il faut respecter les indices et les exposants

question 1  il faudrait justifier le 0,9
par exemple à une baisse de 10% correspond un coefficient multiplicateur de 0,9
Question 2 oui
4a oui,  car on fait l'interprétation et


4c) On pose donc 2 fois la question  !

(v_n) étant une suite géométrique de raison positive plus petite que 1 donc tend vers 0 et u_n vers 50

5 Non, u doit être supérieur à 60 pour que cela puisse s'arrêter
en le mettant inférieur à 60 l'algorithme ne tourne pas puisque vous commencez à 100 donc bien supérieur à 60

même sur une calculatrice ?

exemple sur une TI

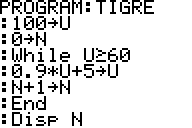
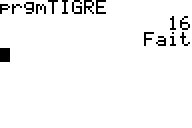
Bonjour hekla

Citation :

Je ne vois pas pourquoi un raisonnement par récurrence

Bonjour malou

La réponse que j'ai donnée ne me satisfaisait pas

par récurrence donc propriété vraie

il existe un k tel que



on applique la propriété de récurrence  

on obtient bien

Pour tout

Là, c'est mieux

oui, là, c'est OK
et ensuite tu démontres qu'elle est décroissante facilement

on peut faire ça en un coup (la double inégalité par récurrence), mais c'est plus lisible en deux coups sans doute

Bonsoir
désoler de répondre que maintenant j'avais cour
1 u=100
2 n=0
3 while u>60
4             u=0,9u +5
5             n=n+1
6 print (n)

ca donne ca pour l'algorithme ?

J'avais vu sur votre autre message  que vous aviez cours jusqu'à 17 h

  Peut-être  je ne connais pas le langage python  normalement cela doit tourner

oui mais le temps de rentrer ca a pris du temps
et d'accord merci donc pour la question b) Quelle est la valeur numérique contenue par la variable n à la fin de l'exécution de ce programme Et donner une interprétation du résultat obtenu
vous ne pouvez pas m'aidez ?

et pour la question 3a)

initialisation :
n=0 u₀=100 u₀>50

Hérédité : Supposons que jusqu'à un entier k , u_k50 et montrons que u_k+1= 0,9u_k+5

je ne comprend pas comment continuer et est ce que ca c'est juste ?

Je vous avais mis le programme fait sur une TI et à côté son résultat

Il donnait pour n 16  C'est le nombre d'années qu'il faudra pour que le nombre de tigres soit inférieur à 60 C'est bien une interprétation dans le cadre de l'exercice du résultat de l'algorithme

Question 3 a)
première partie  montrons que pour tout

or la propriété est vraie pour n=0

Considérons un tel que la propriété et on montre qu'elle est vraie pour



en multipliant les deux membres de l'inégalité par 0,9 nombre positif  on a



on ajoute 5 aux deux membres

est et Par conséquent la propriété est vraie pour

on a montré que la propriété est vraie pour 0 et que si elle est vraie pour elle est vraie pour par conséquent elle est vraie pour tout

pour tout

bonsoir
je conseille à leilaserad de s'entraîner avec cette fiche Le raisonnement par récurrence : principe et exemples rédigés

suite  montrons que

Pour ce faire étudions le signe de la différence



D'après la partie précédente

ah d'accord merci beaucoup
pour la question 3b)
En déduire que la suite (un) est convergente et déterminer sa limite .

je dois mettre que la suite est décroissante et minorée par 50 donc on peut dire qu'elle est convergente c'est ça et pour déterminer sa limite comment faire ?

bonsoir à tous
_{juste un petit message : pour python, normalement si la syntaxe est respectée, ça doit aller.
si problème, j'y jetterai un oeil.
je m'éclipse.}

Oui, décroissante minorée  donc la suite converge
on peut penser que la limite sera 50, mais rien ne le confirme,  c'est l'objet de la question 4 où on prouve bien que la limite est 50

ah d'accord et ducout je met que c'est 50

d'accord merci beaucoup je pense que c'est bon pour cet exercice la je vais tout recopier après et si j'ai encore des questions je reviendrai vers vous

Du coup :    c'est une frappe donnée  pas une dépense

sans problème

bonsoir :
J'ai récris juste pour la question 3a) et 3b) est ce que vous pouvez regarder si c'est bien ça pour la récurrence .

3a)
Initialisation :
n=0 u₀= 100 or 10050 (je ne sais pas d'où ca vient) dont la propriété est vrai pour n=0

Hérédité :
Supposons que jusqu'a un entier k , u_k 50 et montrons que u_k+150


uk50
0,9u_k0,9*50
0,9 u_k+50,9*50+5

La propriété est vraie pour k+1

conclusion la propriété est vraie pour k elle est est vraie pour k+1 par conséquent elle est vraie pour tout n, u_n50

Bonsoir

Parce que c'était demandé

Citation :
a) Montrez par récurrence

d'accord merci

De rien
s'il y a encore des questions, n'hésitez pas

mercii