Inscription / Connexion Nouveau Sujet
( Suite 2 : Exercice 5 ) /!\ Multiples et diviseurs .. /!\
Voilà, le problême est arrangé 
* Tom_Pascal > début ici : 
( Suite : Exercice 5 ) /!\ Diviseurs et Multiples .. /!\ *
La 2b été faite par rapport au lien que Louisa m'a donnée. mais ca ne me dérange pas de la faire pour mieux comprendre 
La 2b été faite par rapport au lien que Louisa m'a donnée
Ah oui en effet, l'explication est bonne tu devrais la comprendre je pense ?
Par contre, je remarque que la 1ère question, tu l'as faite sans utiliser le principe de la décomposition et de l'arbre.
Je reposte l'énoncé ici, sinon faire des aller-retour entre les deux topics ça va être compliqué:
1). Décomposer 750 en produit de facteurs premiers et, à l'aide d'un arbre, déterminer les diviseurs dans de ce nombre.
2). Soient a et b deux entiers et n = 2a x 5b.
a). Quel est le nombre de diviseurs dans 
de n en fonction de a et b.
b). Montrer que n est le carré d'un entier si et seulement si il admet un nombre impair de diviseurs.
Ben tu avais déterminé les bons diviseurs, certes, mais tu n'as pas respecté la consigne puisque cette fois, on t'impose une méthode bien précise.
On va devoir refaire des sciences naturelles si tu vois ce que je veux dire
Je reposte l'énoncé ici, sinon faire des aller-retour entre les deux topics ça va être compliqué:
bonne initiative
Encore décomposer etc ?
Les arbres !
(mais aussi décomposer)Comment on fait pour faire un arbre avec 750 vu qu'il est tout seul ?
D'abord on décompose en facteurs premiers. A toi
Je me suis légèremet ispirée de ce qu'à fait Louisa .. Mais j'ai refais le calcul moi même, et le pire, c'est que ça, j'ai compris 
Mais j'ai refais le calcul moi même, et j'ai compris
J'ai un peu changé ta phrase
Bon passons à l'arbre qui va nous permettre de trouver les diviseurs en question.
Oui mais par contre ça va nous aider à trouver les éléments de l'arbre.
Pour 21, on a 20 et 21
Pour 31, on a 30 et 31
Pour 53, on a 50, 51, 52 et 53
Et là on peut organiser notre arbre.
Oui je vais essayer de magouiller un schéma
20
/
21/
\
\ 21
30
/
31/
\
\ 31
50
/
/______ 51
53/
\_______ 52
\
\ 5 3
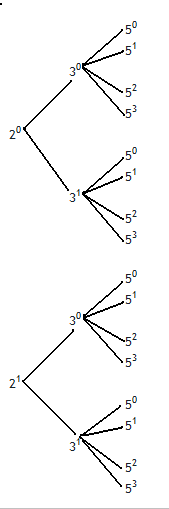
L'arbre donne plutôt :
50
51
30
52
53
20
50
51
31
52
53
50
51
30
52
53
21
50
51
31
52
53
(resterait à dessiner les branches, Louisa si tu passes par là )
Salut
C'est comme pour les piles et les faces, on répertorie tous les cas.
En partant de 20, on peut aller soit sur 30, soit sur 31.
Puis en partant de 30, par exemple, on peut aller soit sur 50, 51, 52, 53
Il y a 16 chemins possibles en tout. D'ailleurs, rappelle-toi, tu avais trouvé 16 diviseurs. Il reste plus qu'à les calculer avec l'arbre.
En fait, ce que je comprends pas, c'est pourquoi par exemple quand on a 30 ont peut aller soit sur 50, 51, 52, 53 et pas sur un 21 par exemple. Ou alors la répartition dans l'arbre se fait au hasard, mais pourquoi il y a plusieurs fois les même .. 
Ah non nn, je viens de comprends on a 20 et 21, donc on a deux branches. Ensuite on met les 30 et 31 dans chaque branche de 2 ( En fait c'est pas le hasard, vu que c'est 2 > 3 > 5 dans l'ordre ), Ensuite dans la décomposition on a eu 53 ce qui nous fait 4 branche en plus pour chaque 5 quelque chose que l'on distribue au 3quelque chose, et le nombres de diviseurs, on doit pas compter tout les branches, mais seulement les dernières, donc celle des 5quelque chose et c'est ce qui donne 16 diviseurs
Les 2 sont sur le même niveau. Une fois qu'on les a quittés, on ne peut aller que sur des 3, qui sont eux aussi sur le même niveau. Et une fois que tu quittes les 3, tu ne peux aller que sur des 5.
Oui et le nombre de branche c'est par rapport au puissance, par exemple si on a 74 on aura 5 branches a ajouter a chaque 5, 70, 71, 72, 73, 74.
Oui on retrouve une des règles : l'exposant + 1
Ici ton exposant vaut 4, donc on a 4 + 1 branches, soit 5
voilà
Donc construire un arbre à partir des facteurs premiers ne te devrait plus te poser de soucis en principe.
Tu dois en être absolument persuadée
(quitte à essayer sur une feuille avec des facteurs premiers pris au hasard)
Alors par exemple :
33 + 52 + 71
Alors on a quatre branches qui sont 30, 31, 32, 33.
A chacune de ces branches, on va en rajouter trois qui sont : 50, 51, 52. ( Remarquons que a chaque fois, on rajoute 1 ).
Puis a chacune des branches 5quelque chose on va rajouter encore 2 branches, qui sont 70 et 71.
Par contre avec le calcul des nombres premiers, quand on a 33 + 52 + 71, on fait comme j'ai dit au dessus.
Mais si on avait : 52 + 33 + 71
On remet dans l'ordre comme mon message de 12h36, ou alors on le laisse dans cette ordre là ?
Ou bien, c'est toujours en ordre croissant automiquement ?
33 + 52 + 71
Attention !
Les facteurs premiers se multiplient ! (d'où leur nom)
Ne m'écris plus jamais ça
Salut Louisa
Pas bien joli mon arbre
Beaucoup mieux que le mien, c'est sympa de l'avoir fait ! Merci
Les facteurs premiers se multiplient ! (d'où leur nom)
Ne m'écris plus jamais ça
Promis
Pas bien joli mon arbre
Mais si il est magnifique
, Merci beaucoup Louisa.
Olivier :
Dans la rédaction de ma réponse, je peux mettre l'arbre, dire le nombre de diviseurs ( 16 ) et mettre aussi les diviseurs que c'est ? C'est-à-dire ce que j'avais trouvée avec Louisa, ou alors il faut juste dire le nombre ?
En fonction de l'arbre :
Par exemple a la branche 20 qui donne sur la 30 on a les branches : 50 qui donne 5 comme diviseurs, la branche 51 qui donne 5 comme diviseurs, la branche 52 qui donne 25 comme diviseurs, et la branche 125 comme diviseurs ?
Quelque chose me dit que c'est faux comme raisonnement, étant donné que de cette manière, on ne trouve pas tout les diviseurs.
On va passer au crible les 16 chemins. Mais 1 à la fois hein
Le premier chemin est : 20 * 30 * 50 = 1 * 1 * 1 = 1
1 est le premier diviseur
Je te rappelle qu'un nombre élevé à la puissance 0 vaut toujours 1
Annuler
connectez vous