Inscription / Connexion Nouveau Sujet
Suite
Bonjour
Je suis bloqué sur un exercice de mon DM, en esperant que vous pouvez m'aider.
En 2002, la ville U comptait 50 000 habitants alors qu'il y en avait que 30 000 dans la ville V.
Depuis la ville U voit sa population augmenter de 2000 habitants par an et pour la ville V la croissance annuelle est de 6%.
Soit Un la population de la ville U et Vn celle de la ville V l'année 2002 + n
Ainsi U0=50 000 et V0= 30 000.
Etude de la suite Un
a) Calculer u1 et u2
-> u1 = 50 000 + 2 000 = 52 000
u2 = 52 000 + 2 000 = 54 000
b) Préciser en justifiant, la nature de la suite Un
-> C'est une suite Arithmétique.
c) En déduire l'expression de Un en fonction de N et calculer la population de la ville U en 2012
-> Un=Un+2 000
En 2012 il y avait 70 000 habitants.
d) Quel a été le pourcentage d'évolution de cette population entre 2002 et 2012 ?
-> Je n'y arrive pas.
2) Etude de la suite Vn
a) Prouver que la suite Vn est géométrique et préciser sa raison
-> La suite est géométrique car on passe d'un terme à un autre en multipliant toujours par le meme nombre.
La raison est 6%
b) En déduire que pour tout entier naturel n, on a Vn = 30 000 x 1.06n
-> Je ne sais pas
c) Calculer le nombre d'habitants dans la ville V en 2012
-> Je ne sais pas
Merci beaucoup pour votre aide
Bonjour
d'accord
expression de en fonction de
vous ne répondez pas à la question et vous écrivez 0=2000 en simplifiant par
Calcul d'un taux d'évolution
u2 = 54 000 ou 52 000 comme vous l'avez ecrit ?
De plus le taux d'évolution, c'est pour quelle question svp?
erreur sur les indices
d) Quel a été le pourcentage d'évolution de cette population entre 2002 et 2012 ?
Du coup, Valeur Finale - Valeur initiale / Valeur Initiale
=( 70 000 - 50 000 ) / 50 000 * 100
= 40 %
C'est bien ça?
Non la relation de récurrence est et en explicite en fonction de
Vous donnez une forme qui ne dépend pas de
partie suite géométrique
la raison est le coefficient multiplicateur associé à une augmentation de et non
ou 0,06
b ) c'est dans le cours
c) n=10
Je ne sais pas comment est l'expression Un du coup :/
b) dans mon cours c'est juste écrit que dès qu'il s'agit d'une suite géométrique, on a toujours un entier naturel * la raison
donc ici, 30 000 habitants * par 1.06 , la raison
Mais je ne sais pas comment répondre correctement à la question
je l'ai écrit vous avez une suite arithmétique de raison 2000 et de premier terme 50000 Il n'y a plus qu'à remplacer dans
Vous avez une suite géométrique de raison 1,06 coefficient multiplicateur lié à une augmentation de
on a donc ,
etc donc
D'accord
la B du coup c'est ce que vous avez écrit plus haut
on a donc v_1= qv_0, v_2=qv_1=v_0 q^2\quad v_3=qv_2= v_0q^3 etc donc vn=v0qn
C) Vn=30 000 * 1.06n
Et on multiplie le résultat par 12 ?
a) raison 1,06 coefficient multiplicateur associé à une hausse de 6 %
b) donc
2012= 2002+n donc
Population en 2012 on remplace par 10 D'où sort 12 ?
C'est bien d'avoir pensé à arrondir mais il s'agit ici de population, un arrondi à l'unité aurait été préférable
Ah d'accord, merci beaucoup
d) (( Valeur Finale - Valeur initiale ) / Valeur initiale ) * 100
= (( 53 725 - 30 000 ) / 30 000) *100
=79.08 %
C'est bien ça?
Il ne faut pas multiplier par 100 ou alors il faut aussi diviser par 100
Ainsi oui
sinon après vous pouvez dire que l'augmentation est de
en plus rapide le coefficient multiplicateur est de 1,06^{10} donc le taux d'évolution
La question était posée pour la suite arithmétique pas pour la suite géométrique
D'accord merci
Donc le pourcentage d'évolution de la population de la ville V est de 79.08%
J'ai encore quelques questions svp
a) déterminer les formules tapées en C3 qui permettraient de compléter la colonne C. =C2*1.06^A3
=C$2*(1+E$2)^A3
=C2*(1+E2)
=$C$2*1.06^A3
J'ai essayé sur le tableur.
Je pense que les formules correctes sont la deuxième et la dernière, mais je ne sais pas comment le justifier
Pouvez-vous m'aider svp?
La seule qui ne convient pas est la deuxième Si en C3 on a bien le résultat convenable ce n'est plus le cas après
en C4 on aurait =C3*(1+E3) = C3*1
La première convient car la ligne 2 a été bloquée par $ Cela ne fonctionnerait pas si on tirait vers la droite c'est-à-dire en changeant de colonnes
La dernière convient aussi puisque l'on a une référence absolue et on multiplie par
Je n'avais pas vu la première car étant isolée
Celle-ci ne convient pas puisque ne fait pas référence à une cellule fixe
En reprenant c'est donc la 2 et la 4
D'accord merci beaucoup pour la justification 
J'ai une dernière question svp.
"En utilisant la calculatrice, et en expliquant la démarche, déterminer à partir de quelle année la population de la ville V devient supérieur à celle de la ville U."
Avec le tableur, je pense savoir répondre à cette question, mais avec la calculatrice je ne sais pas:/
Merci
Deux possibilités
faire tracer les deux courbes et lire l'abscisse du point d'intersection à partir de laquelle la courbe représentative de v est au dessus de celle de u
utiliser la calculatrice avec le mode table. Ce qui revient évidemment à utiliser le tableur
Comme vous avez commencé avec le tableur autant continuer
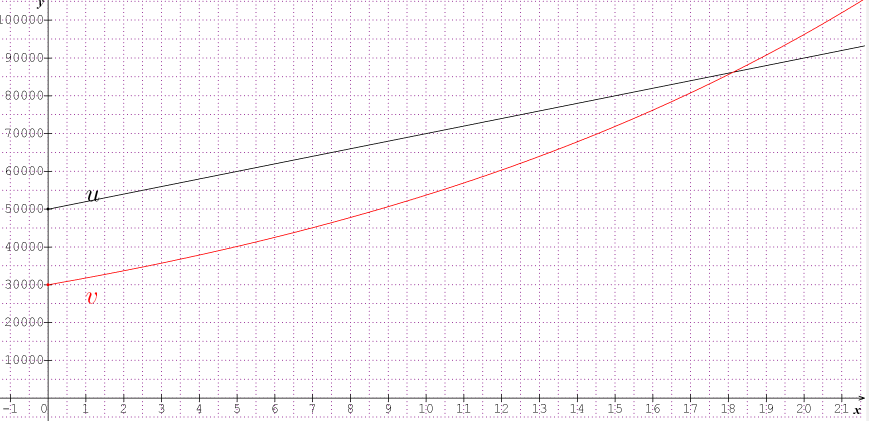
D'accord merci beaucoup
Une toute dernière question svp, j'aimerais être sur de ma réponse,
Pour la question 1c)
J'ai mit " Un=U0+nr , soit Un=U0+2000"
C'est bien ça svp?




