Inscription / Connexion Nouveau Sujet
suite avec fonction
Bonsoir,
voici un exercice que l'on doit faire, je vais déjà mettre le début
On considère la suite (un) définie par u0=1/2 et telle que pour tout entier naturel n
un+1=(3un)/(1+2un)
1) soit f la fonction définie sur [0;+infinie[ par f(x) (3x)/(2x+1)
on a tracé, en annexe (à rendre avec la copie) la courbe C représentative de f et la droite D d'équation y=x
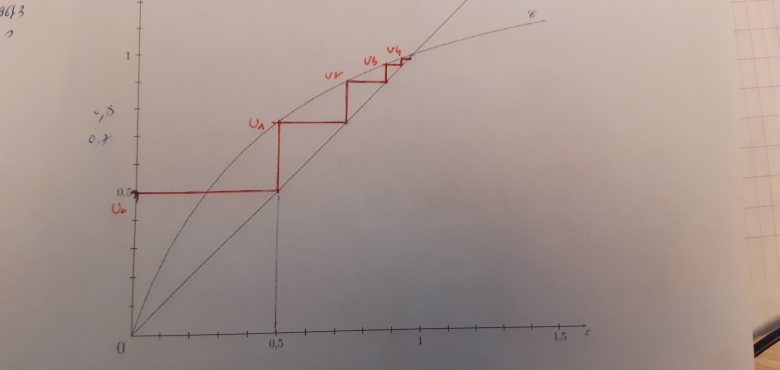
Placer sur l'axe des abscisses uo,u1 ,u2, u3 et u4 en faisant apparaître les traits de construction
Je ne sais comment faire
j'ai calculer u1,u2 u3 et u 4
up=0,5
u1=0,75
u2=0,90
u3=0,9643
u1=0,9878
merci de m'expliquer comment je dois faire (nous n'avons pas vu d'exemple de ce type)
MERCI
bonjour,
considère que l'axe des ordonnées porte Un :
U0 = 1/2 place le point (0 ; 1/2).
ensuite, pour calculer Un+1 = f(Un), on doit replacer la valeur de Un sur l'axe des abscisses, pour cela : trace la // à l'axe des abscisses passant par U0 (y=1/2). jusqu'à ce qu'elle coupe la droite y=x, puis "redescends" vers l'axe xx' ==> tu vas te retrouver en x=1/2.
tu y es ?
Re,
j'ai beaucoup de mal
car sur les abscisses ça va de 0,1 en 0,1
je dois donc mettre combien de points je suis perdue
j'ai mis des petits points sur 0,5 sur les x et 0,75 sur les y mais je dois en mettre combien de points car l'exercice me dit u0 ; u1; u2 , u 3 et u4
quelles valeurs représente (en u) 0,5 et 0,75
MERCI
mmhh... as tu fait ce que je t'ai recommandé ?
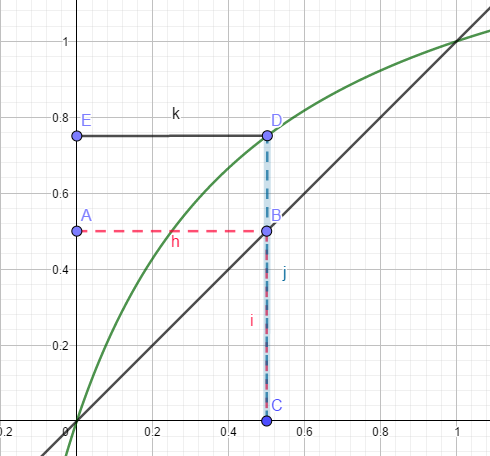
regarde cette figure :
en A, on a U0.
pour placer U0 sur l'axe des abscisses, je trace AB (B est sur la droite d'équation y=x), puis AC : sur l'axe des abscisses, en C j'ai alors la valeur de U0.
je cherche ensuite à connaître la valeur de U1 = f(U0) : je trace CD, D appartient à la courbe, puis DE pour trouver f(u0) et en E, j'ai U1.
ca te va ?
tu as la méthode expliquée là si tu veux ![]()
tu dessines la courbe (ici y=3x/(2x+1)) et la droite y=x qui sert à rabattre les points de l'axe des y sur l'axe des x pour pouvoir continuer la récurrence. Les segments semblent rebondir un coup sur la courbe et un coup sur la droite; A chaque verticale bleue, il y a un terme de la suite.
Donc ici on voit une suite croissante qui tend vers 1.
Re,
merci à vous deux mais on n'a jamais fait ça en cours.
Je vais regarder demain A.M. car j'ai du travail demain jusque 16 h 3
MERCI
Re,
OK à demain mais on regardant les deux croquis j'ai du mal à comprendre
ce que je ne comprends pas c'est qu'il est noté
Placer sur l'axe des abscisses uo,u1 ,u2, u3 et u4 en faisant apparaître les traits de construction
je voulais savoir ce qu'était donc là u0,u1,u2,u3 et u4
bonne soirée et à demain
je crois que tu ne comprends pas parce que tu ne lis pas bien les aides.
"pour placer U0 sur l'axe des abscisses, je trace AB (B est sur la droite d'équation y=x), puis AC : sur l'axe des abscisses, en C j'ai alors la valeur de U0."
U0 est ainsi placé sur l'axe des abscisses.
U1 = f(U0) : en t'appuyant sur la courbe, tu peux placer U1 sur l'axe des ordonnées, puis en utilisant la droite d'équation y=x, tu rabats U1 sur l'axe des abscisses.
ensuite U2 = f(U1). en t'appuyant sur la courbe, tu peux placer U2 sur l'axe des ordonnées, puis en utilisant la droite d'équation y=x, tu rabats U2 sur l'axe des abscisses.
et ainsi de suite.
au final, tu as tous les Un sur l'axe des abscisses.
Bonne soirée.
Re,
pour moi ce que j'ai mis en rouge c'est pour répondre à la question qui était :
1) soit f la fonction définie sur [0;+infinie[ par f(x) (3x)/(2x+1)
on a tracé, en annexe (à rendre avec la copie) la courbe C représentative de f et la droite D d'équation y=x
Placer sur l'axe des abscisses uo,u1 ,u2, u3 et u4 en faisant apparaître les traits de construction
MERCI
Bonjour,
Je réponds en l'absence de Leile et Glapion.
Placer sur l'axe des abscisses
N'écris pas u1, u2, u3 et u4 sur la courbe.
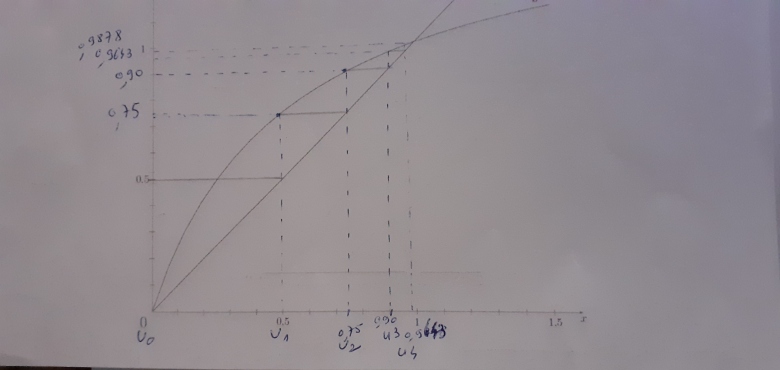
Mais prolonge les traits rouges verticaux jusque l'axe des abscisses ; et tu pourras y écrire u1, u2, u3 et u4 sous les intersections obtenues.
bonjour,
oui, c'est ça mais tu as décalé : tu as mis U1 en 0,5 alors que c'est U0 qui vaut 1/2.
U0 n'est pas en 0. et c'est U1 qui est en 0,75
et ainsi de suite.
Oui, c'est mieux.
Encore mieux si tu écris u2, u3 et u4 sur l'axe des ordonnées et pas des valeurs approchées.
As-tu compris pourquoi les termes peuvent se construire ainsi ?
Re,
ok je refais
j'ai compris quand faisant les escaliers un point d'intersection de la courbe on avait la valeur de f(x) et en abaissant on trouve la valeur des u
en attendant de refaire je poursuis
2) a) calculer u1 et u2
j'ai trouvé u1=0,75
et u2=0,90
et en abscisse on a bien u1 en 0,75
b) démontrer, par récurrence que pour tout entier naturel n, 0<un
j'ai toujours beaucoup de mal avec ça
donc
initialisation
u0=1/2 et donc l'inégalité est vraie quand n=0
hérédité
soit n 0. Supposons que un>0 et montrons que v(n+1)>0
0. Supposons que un>0 et montrons que v(n+1)>0
comme u (n+1)= 3un/1+2un et que un>0 on a u(n+1)>0
conclusion
on a montré par récurrence que pour tout entier n, un>0
3)On admet que pour tout entier naturel n, un<1
a) ddémontrer que la suite (un) est croissante
je sais qu'il y a deux méthodes mais je ne sais jamais laquelle choisir
soit u(n+1)- un ou u(n+1)/un
je voulais faire
u(n+1)/un
soit 3un/(1+2un) le tout diviser par 34(n-1)/(1+2u(n-1)
donc je multiplie par l'inverse
3un/1+2un * 1+2u(n-1)/3u(n-1)
et après je ne sais pas faire
MERCI
Re,
donc
3un/1+2un -3u(n-1)/1+2u(n-1)
je mets tout au même dénominateur
au numérateur j'ai 3un(1+2un)-(3un-1)(1+2un)
au dénominateur j'ai (1+2un)(1+2u(n-))
mais après ça coince
MERCI
Re,
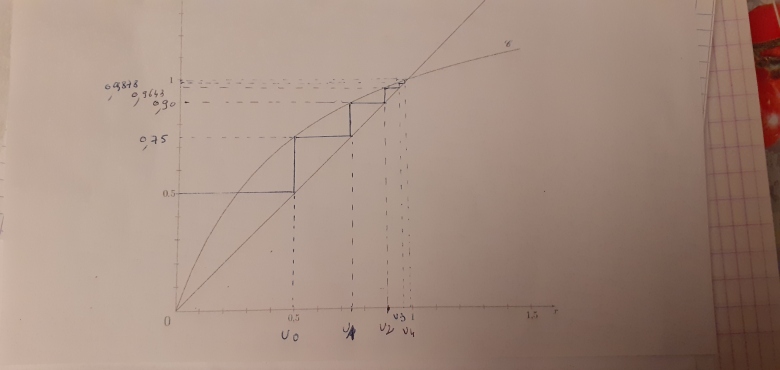
voici le dessin rectifié.
pour la suite
je suis arrivée à
u(n+1)-un= numérateur 2un(1-un)
dénominateur 1+2un
je ne sais pas comment continuer
je sais que 0<un<1 est-ce que parce que le numérateur et dénominateur sont positifs je peux dire que un+1-un>0 ?
Ensuite ça a été à part la fin que je vous mets
soit (vn) la suite définie, pour tout entier naturel n, par vn=un/1-un
a) montrer que la suite (vn) est une suite géométrique de raison 3 (j'ai vu le corrigé donc c'est bon) mais auriez-vous une méthode pour savoir si la suite est géométrique ou arithmétique
b) exprimer pour tout entier naturel n, vn en fonction de n
c'est ok
c) en déduire que, pour tout entier naturel n, un=3n/3n+1
c'est ok aussi
d) sachant que lim 3n = + infini et que lim (1/3)n = 0
x tend vers plus infini x tend vers plus l'infini
déterminer la limite de la suite (un)
et là je ne comprends pas avec la correction que j'ai vu sur un site
c'est noté :
(1+3n)/3n = 1/3n +1 or lim 1/3n = 0 (car 3>1)
n tend vers plus l'infini
par conséquent
lim 1/un = lim (1+3n)/3n =1 et lim un = 1
n tend vers plus l'infini n tend vers plus l'infini n tend vers plus l'infini
j'ai oublié de noté que la question b) je suis arrivée comme eux à 3n=un+3uun mais après je ne sais pas comment ils ont fait c'est noté
un=3n/(1+3n)
MERCI pour vos explications
Re bonjour,
en recopiant ce que j'ai fait et en regardant le corrigé je n'ai pas compris
à la question 4c) en déduire que, pour tout entier naturel n, un =(3n)/(3n+1)
je trouve comme eux jusque
3n=un+3nun
après ils mettent
un=(3n)/(1+3n) mais je ne sais pas comment ils ont fait
si quelqu'un veut bien m'expliquer ?
ET pour la dernière question sur les limites
MERCI BEAUCOUP
Re,
pour la question c) j'y suis arrivée en prenant vn=un/(1-un)
4d) ce sont les limites
sachant que lim 3n = + infini et que lim (1/3)n = 0
x tend vers plus infini x tend vers plus l'infini
déterminer la limite de la suite (un)
et là je ne comprends pas avec la correction que j'ai vu sur un site
c'est noté :
(1+3n)/3n = 1/3n +1 or lim 1/3n = 0 (car 3>1)
n tend vers plus l'infini
par conséquent
lim 1/un = lim (1+3n)/3n =1 et lim un = 1
n tend vers plus l'infini n tend vers plus l'infini n tend vers plus l'infini
MERCI de me répondre
bonjour,
je te réponds rapidement (je travaille, je ne pourrai pas rester).
pour la limite
tu peux aussi dire que qd x tend vers +oo,
limite de (3n + 1) = limite (3n)
(en l'infini, rajouter 1 à 3n n'a pas de poids)
et conclure lim = 1
je file, bonne journée,