Inscription / Connexion Nouveau Sujet
Suite de pointe sur graphique
Bonjour,
Je viens vers vous pour vous demander un peu d?aide concernant un exercice préparatoire à un Devoir Surveillé que ma professeur m?a transmis vendredi.
Il faut premièrement savoir que la parabole C est d?équation y=x^2 et que le point A0 appartient à C et a pour coordonnées (1;1).
Les points An et Bn seront construits de la façon suivante:
- Les droites (A0B0), (A1B1),? (AnBn) ont toutes la même pente -1/5.
-Les droites (B0A1), (B1A2),? (BnAn+1) ont toutes la même pente 1/4.
À savoir qu?on note an l?abscisse de An et bn l?abscisse de Bn.
Premièrement, j?ai dû construire les points B2 et A3. Pour cela, j?ai tracé les parallèles des droites déjà tracées afin de construire B2 et A3, puis par lecture graphique, j?ai déduit b2=(env.) -2,1 et a3=(env.) 2,4.
Ensuite, on m?a demandé de déterminer a0 et b0; comme a0 était donné dans l?énoncé, j?ai dit que a0=1, et pour b0, je n?ai pas trouvé de solutions par calcul, j?ai donc établi b0 par lecture graphique (je ne sais pas si c?était la bonne manière).
On le demande ensuite de démontrer que ptt nEN, an+Bn=-1/5 et an+1+Bn=1/4.
Ça me parait finalement assez logique mais je ne sais pas comment le démontrer avec des calculs? Peut être une démonstration par récurrence?
Je vous remercie!
Pour le « 1) », j?ai établi qu?en lisant le graphique, b2=4,4 et a3=5,5
Pour la 2), toujours par lecture graphique, j?ai trouvé que a0=1 et b0=-1,25.
Pour la « 3 ) » je comptais utiliser une démonstration par récurrence, mais finalement je bloque et ne sais pas quoi utiliser; et j?ai le meme probleme pour la « 4) ».
PS: le graphique est transmit en Pj
Je vous remercie pour votre aide!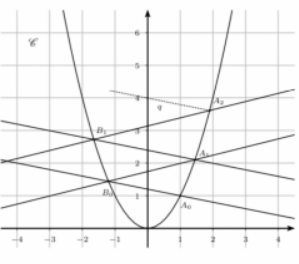
* modération> Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum Ntiooo,  *
*![]() A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien)
A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien)
salut
certes une image d'un graphique est autorisée ... mais sûrement pas celle de l'énoncé qui est recopié correctement ici ...
Bonjour, faudrait-il que je supprime l'image et vous retransmette uniquement le graphique? Je suis désolé je n'étais pas au courant de cela
Bonjourà tous les deux
Ntiooo, recopie ton énoncé s'il te plaît (j'ai recadré ton image)
Fais le en réponse à ce message
Bonjour,
Bonjour,
Je viens vers vous pour vous demander un peu d?aide concernant un exercice préparatoire à un Devoir Surveillé que ma professeur m?a transmis vendredi.
Il faut premièrement savoir que la parabole C est d?équation y=x^2 et que le point A0 appartient à C et a pour coordonnées (1;1).
Les points An et Bn seront construits de la façon suivante:
- Les droites (A0B0), (A1B1),? (AnBn) ont toutes la même pente -1/5.
-Les droites (B0A1), (B1A2),? (BnAn+1) ont toutes la même pente 1/4.
À savoir qu?on note an l?abscisse de An et bn l?abscisse de Bn.
Premièrement, j?ai dû construire les points B2 et A3. Pour cela, j?ai tracé les parallèles des droites déjà tracées afin de construire B2 et A3, puis par lecture graphique, j?ai déduit b2=(env.) -2,1 et a3=(env.) 2,4.
Ensuite, on m?a demandé de déterminer a0 et b0; comme a0 était donné dans l?énoncé, j?ai dit que a0=1, et pour b0, je n?ai pas trouvé de solutions par calcul, j?ai donc établi b0 par lecture graphique (je ne sais pas si c?était la bonne manière).
On le demande ensuite de démontrer que ptt nEN, an+Bn=-1/5 et an+1+Bn=1/4.
Ça me parait finalement assez logique mais je ne sais pas comment le démontrer avec des calculs? Peut être une démonstration par récurrence?
Je vous remercie!
**énoncé recopié dans le premier message pour une meilleure lisibilité de l'exercice **
une lecture graphique ne me semble pas suffisante !!
ne sais-tu pas déterminer l'équation réduite d'une droite connaissant un point et son coefficient directeur ?
et cela te servira pour tout le pb en généralisant avec n ...
Ntiooo, je vais te demander d'aller mettre un message sur l'autre site, que tu n'as plus besoin d'aide
sinon, je ferme la discussion ici
Je sais que y=ax+b
Donc avec le point A0 (1;1), en sachant que y=x^2, et que le coeff directeur est -1/5:
1=-1/5 * 1 + b
b=6/5=1.2
Donc l?équation de la droite est y= -1/5x + 1.2 ?
malou edit> ** discussion fermée pour le moment **
discussion réouverte
Donc pour trouver b0, j'utilise cette formule pour trouver y de B0, puis j'utilise y=x^2 afin de trouver b0:
b0= racine(yB0)
Mais une fois que j'ai trouvé cela, je ne comprends toujours pas comment démontrer que ptt nEN, an+bn=-1/5
Finalement, même avec cette équation réduite, ne connaissant aucune coordonnée de B0, je ne peux pas l'utiliser afin de déterminer b0; je ne vois pas en quoi elle pourrait m'être utile, et ne m'aide pas pour la démonstration de an+bn=1/5 et an+1 + bn=1/4…
tu connais les coordonnées du point A_0
tu connais la pente de la droite(A_0 B_0)
ne sais-tu pas déterminer son équation ?
Comme je l'ai dit,
L'équation de la droite serait y= -1/5x + 1.2
Mais cela ne me permet pas de déterminer b0…


 ) :
) :

