Inscription / Connexion Nouveau Sujet
suite récurrente d'ordre 2
Bonjour, j'ai un petit problème avec mon dm de maths.
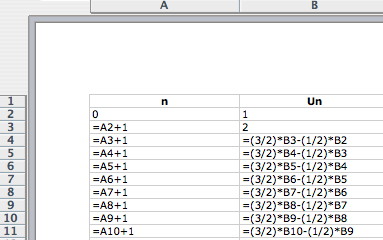
On considère la suite réelle u définie par ses deux premiers termes: u0=1 et u1= 2, et par la relation , pour tout n de 
:
un+2= 3/2 un+1 - 1/2un.
1. Utiliser une calculatrice ou un tableur pour émettre une conjecture concernant le sens de variation et la limite de la suite u.
2. Soit v la suite réelle définie par vn= un+1-un pour tout n de .
Démontrer que la suite v est une suite géométrique.
Exprimer le terme général vn en fonction de n.
3. En déduire l'expression du terme général un en fonction de n.
4. Valider les conjectures émises à la question 1.
5. On appelle 
la limite de la suite u. Déterminer le plus petit entier n0 tel que : pour tout entier n
n0 |un-| < 10-3.
Pouvez vous m'aider sur tout le dm car je n'ai vraiment rien compris je n'arrive même pas à rentrer la suite sur excel et pour le reste je bloque vraiment.... 
Merci beaucouo de votre aide =)
oui c'est ce que j'avais fait mais cela me donne une suite super compliquée et non une constante..
Les suites qu'on étudie sont rarement constantes !
Que trouves tu pour Vn+1 ?
Et bien je trouve que vn+1 = 3/2un+1 - 1/2un-(2/3un+2 + 1/2un) et donc la je ne suis pas très convaincue...
Tu as raison de pas être très convaincue...
Tu remplaces Un+2 par ce que vaut Un+2
mais tu laisses bien tranquille - Un+1 ; pourquoi veux tu le remplacer par quelque chose de faux !!!
Un+2 - Un+1 = .... - Un+1 = .....
Tu sais ajouter 3/2 de quelque chose à -1 fois quelque chose ?
(3/2)x - x = ??? x
donc (3/2)Un+1 - Un+1 = ???Un+1
Donc (3/2)Un+1 - (1/2)Un - Un+1 = ???Un+1 - (1/2)Un = (1/2) [ ??? - ????]
ah ouiiii oulala je m'emmêle les pinceaux =S d'accord j'ai compris maintenant merci beaucoup dsl d'être aussi bête :').
Donc pour exprimer v après c'est facile c'est ce qu'on a fait en cours avec la formule vn= v0
qn.
Puis pour un, il faut que je fasse en fonction de ce que j'ai trouvé pour vn c'est ça ?
Quand ils disent valider faut-il démontrer ?
Par contre pour la q° 5 je ne sais absolument pas...
Dsl de toutes ces questions je dois être chiante mais en tout cas un grand merci =')
Oui il faut trouver Un en fonction de n en partant de ce que tu trouves pour Vn
Et valider veut bien dire démontrer la conjecture faite au début.
meerci pour Vn j'ai trouvé maais je n'arrive pas à exprimer Un en fonction de n comment je peux faire s'il vous plaît ?
hmmmm je ne vois pas trop quoi faire avec ça... c'est bien la formule de Un ? Quand j'essaye de calculer la limite je ne trouve pas 3....
Tu vas bien arriver à démontrer cette égalité par récurrence !
Dans cette expression, tu reconnais la somme des premiers termes d'une suite géométrique !
Quelle est sa valeur ? Quelle est la limite de cette somme à l'infini ? Ne serait-ce pas 2 ?
Oui mais à la 1ère question lorsqu'il demande de conjecturer la limite de Un on trouve sur le tableur que sa limite est 3 car c'est une suite convergente vers 3. Or là si je prouve que ça limite est 2 cela ne sera pas cohérent avec la limite que j'ai trouvé sur excel et toutes les autres personnes de ma classe ont trouvé que la limite est 3...
Un = U0 + la somme des premiers termes d'une suite géométrique
donc limite de Un = U0 + la limite de la somme des premiers termes de la suite géométrique
c'est à dire 1 + 2 = 3
D'accord je n'avais pas pris cela dans ce sens c'est bon j'ai compris ! =) merci beaucoup ! Désolé de vous déranger une nouvelle fois mais pour la question 5, je ne vois pas non plus comment faire... Auriez-vous une piste à me donner s'il vous plaît ? Merci beaucoup de votre aide et de votre patience !!
Annuler
connectez vous