(Hn) est une suite géométrique de raison 1/2

Bonjour

bonjour,

tu bloques ?  
"La balle rebondit en n'atteignant à chaque fois que la moitié de la hauteur du rebond précédent"
au départ hauteur = 1000 cm
à ton avis au coup suivant , hauteur = ?

toureissa,
donner  une réponse c'est facile      , aider lilia0 à la trouver elle-même, c'est beaucoup mieux !

1005

Mais je n'arrive pas à exprimer Hn+1 et Hn

500..?

Ah super je viens de comprendre U2 vaut 250

Hn+1 = Hn x 0,5 puissance n

et Hn =1000x0,5 puissance n

H0=1000
H1=500
H2 = 250  
oui,

H _n+1 = 0,5  H_n   (pas de puissance ici !!)

Hn =  1000 *  0.5 ⁿ     : OK

Super merci à vous je me suis élaboré un algorithme  afin qu'il donne le nombre de rebonds nécessaires avant que la hauteur atteinte ne soit inférieure à 2cm

Je dois remplir le trou soit tant que Hn >
H=1000
N= 1/2

"je me suis élaboré un algorithme"
??

Faut de Frappe

que proposes tu pour compléter cet algorithme ?

B2 = -1
B3 = -1-3*A3

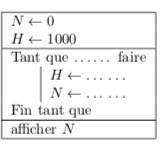
tu calcules les hauteurs successives tant que cette hauteur est > 2

quand tu écris  H n+1 = Hn * 0.5
tu dis "nouvelle valeur de la hauteur =  moitié de l'ancienne valeur "

dans ton algo, c'est pareil
tant que la hauteur est > 2
je calcule la valeur suivante :   H prend la valeur de la moitié de H.

et pour n : c'est le nombre de rebonds. A ton avis, qu'est ce que tu mets pour compter un rebond de plus à chaque fois que tu passes dans la boucle ?

X 1/2

lilia0, je ne comprends rien à tes réponses..
en terminale, tu pourrais quand même écrire quelque chose de complet, une égalité..
exprime toi correctement, stp.

désolé je récapitule

1) Tant que >2
Faire H : 1000
N : 1/2

si tu laisses   H =1000,    la valeur de H ne bougera pas..
il faut écrire   H  devient   H/2   dans la boucle

et n=1/2  ??   je ne comprends pas..
à chaque tour dans la boucle , n est augmenté de 1
==>  n devient n+1
..

Oh super merci !

N <-- 0
H <-- 1000
tant que H > 2   faire
       H <--    H/2
      N  < --   N + 1
fin tant que
afficher N

Bonne soirée.