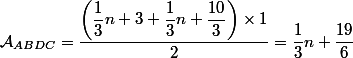Inscription / Connexion Nouveau Sujet
Suites
Bonsoir, voilà j'ai un exercice à faire et je ne parviens pas à comprendre le raisonnement pour la question 1 . Si quelqu'un pouvait m'aider ça serait génial ☺️
Voici l'énoncé
An et Pn sont respectivement l'aire et le périmètre du domaine en gris sur la figure cicontre dans un repère orthonormé.
1. Exprimer a, et p, en fonction de n.
2. Démontrer que les suites (an) et (Pn)
n n+1 sont arithmétiques.
Le graphique est avec le post 🙃
En vous remerciant pour l'aide que vous pourrez m'apporter !
Bonsoir,
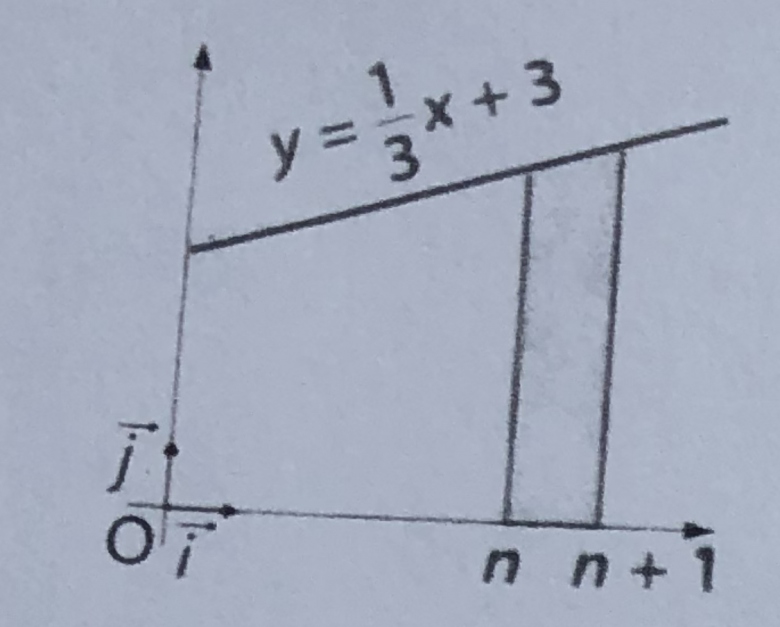
Commence par nommer les points, par exemple :
A(n,0)
B(n+1,0)
C le point à la verticale de A sur la droite inclinée
D le point à la verticale de B sur la droite inclinée.
Commence par déterminer les coordonnées de C et D.
Pour l'aire, il faudra que tu te souviennes d'un certain théorème sur la surface d'un trapèze.
Pour le périmètre, il faudra que tu détermines les longueurs des quatre côtés. Trois des quatre seront très faciles, le quatrième CD sera un peu moins facile, quand tu seras là on t'aidera.
Bonjour,
Désolé de ne répondre que maintenant je vous répond donc à ma pause midi
J'ai mis les coordonnées de C(5;5,5) et D (6,5;6)
Est ce bon ?
Ensuite la formule du trapèze est (B+b)xH2
Mais je ne vois pas comment l'utiliser comme c'est en écriture littérale
J'ai bien modifié mon profil ☺️
Ah oui d'accord je comprend mieux
Je n'ai pas compris la question « que valent AC et BD »
Et cela me bloque pour l'air et le périmètre
Ahh oui la formule des coordonnées,! Bon et bien dès que j'ai un moment j'essaie et je vous redis
Si je m'absente quelque temps c'est que je suis au lycée ou dans les transports en commun, je m'en excuse. Merci de votre aide ☺️
Je suis de retour ! Jusqu'au coucher  je vous préviendrais
je vous préviendrais
Donc la formule de la distance il faut remplacer par les coordonnes de C et D mais comment puis je calculer ca car il y a des" n et n=1" ..?
Tout l'exercice comportera des
Puisque (AC) et (BD) sont parallèles à l'axe des ordonnées la distance entre les deux points n'est donc que la différence des ordonnées
Ok merci beaucoup monsieur, j'ai encore jusqu'à lundi pour faire mon DM je vous redis ce que je trouve demain
Belle soirée à vous, et merci
En simplifiant l'expression Aire abcd
Je suis un peu perdue …
Comment avez vous obtenu cette simplification et à quoi va t -elle servir..? Calculer l'aire ?
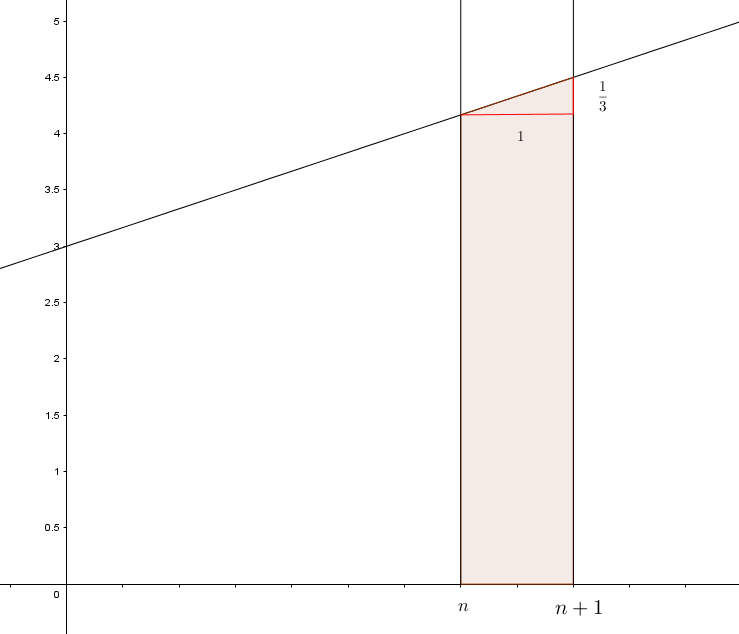
On cherche à calculer l'aire de la partie grisée sur votre dessin
Il s'agit bien d'un trapèze ici en outre il est rectangle
la petite base est AC soit
la grande base est BD soit
La hauteur est AB soit 1
d'où ce que j'ai tapé
Maintenant on effectue les calculs.
D'où le résultat pour l'aire du trapèze
Ahh oui je comprends mieux d'où vient le résultats merci beaucoup!
Donc sachant que Pn est le périmetre il faut additioner les longueurs mais je ne sais pas quelle méthode utilisée ..?
Quelle méthode ?
Le périmètre est AB +BD+DC+CA
Il vous reste DC à calculer vous connaissez les autres longueurs
J'ai peut-être une piste...
Comme le trapeze est egalement formé d'un triangle rectangle, peut etre que je peux calculer son hypotenus puis additioner au rectangle restant.
Mais je ne sais pas vraiment comment m'y prendre
Si vous pensez au triangle rectangle dessiné les longueurs sont inscrites sur la figure sinon vous avez encore la relation écrite hier 13 :14
Si je me sers de la figure, je fais donc 1² puis1/3² =10/9 suis je sur la bonne voix ou pas du tout ?
Je pense continuer cet exercice demain. Car la je sature avec la fatigue, je reviens demain à tête reposé si vous pouviez juste me dire si je suis sur la bonne voie ou dans le cas contraire m'indiquer comment je pourrais m' prendre ca serait génial!
Belle soirée a vous, encore merci et à demain 
Ah oui mince, cela donne 1.05409
J'arrondis ? Comment faire pour exprimer le périmètre du rectangle grâce à ça ?
D'accord après simplification je trouve ceci
« 22/3+1/3n+√10/3x1/3n » est ce bon ? Si oui c'est donc ça qui correspond à Pn ?
Autre petite question.. dans votre message de 12:48 aujourd'hui
Vous avez mis apres « on effectue les calcul »
Il y a 3+10/3 et vous avez mis ensuite dans le résultat final 19/3 ne serait ce pas 13 ? Car je ne comprend pas l'origine du 19
Comment arrivez vous à cette simplification de Pn ?
J'avais juste oublier d'effacer n n+1 je m'en excuse
Il y a seulement 2 questions la deuxième étant « 2.démontrer que An et Pn sont arithmétiques »
Ah oui ok je comprend beaucoup mieux merci
Lorsque vous m'avez dis il y a un + qui se transforme en x de quoi parliez vous ?
« 22/3+1/3n+√10/3x1/3n » est ce bon ?
De ceci le signe d'addition est devenu un signe de multiplication
Ah oui je pense que je vais les revoir j'avais oublier qu'il fallait changer le dénominateur.. Merci!!
Comment puis je faire pour démontrer avec ces 2 valeurs de An et Pn



 équivalences des systèmes de niveaux scolaires
équivalences des systèmes de niveaux scolaires