Inscription / Connexion Nouveau Sujet
Suites
Bonjour
Au début de l'année 2021, une colonie d'oiseaux comptait 40 individus. L'observation conduit à modéliser l'évolution de la population par la suite Un définie pour tout entier naturel n par:
U0= 40
Un+1= 0,008Un (200-Un)
où Un désigne le nombre d'individus au début de l'année (2021 + n)
1. Donner une estimation, selon ce modèle, du nombre d'oiseaux dans la colonie au début de l'année 2022
51,2
On considère la fonction f définie sur l'intervalle [0; 100] par f(x) = 0,008x(200 - x) .
2. Résoudre dans l'intervalle [0;100] l'équation f(x) = x .
X1= 0 X2=75
3.
a. Démontrer que la fonction f est croissante sur l'intervalle (0; 100) et dresser son tableau de variations.
Strictement Croissante sur [0,100]
b. En remarquant que, pour tout entier naturel n, un + 1 =f(un ) démontrer par ré currence que, pour tout entier naturel :
0 <= Un<=Un+1 <=100.
je l'ai démontrer
c. En déduire que la suite Un est convergente Soit l sa limite
On Applique le théorème de convergence monotone
d. On admet que l =125. Interpréter le résultat dans le contexte de l'exercice.
Voici la q° pour laquelle j'ai besoin d'aide :
J'ai remarqué que dans la q° 1 à lorsqu'on résout l'équation on a 200x-x2 = 125x mais je ne sais pas comment l'interpréter
Merci de votre aide
Bonjour
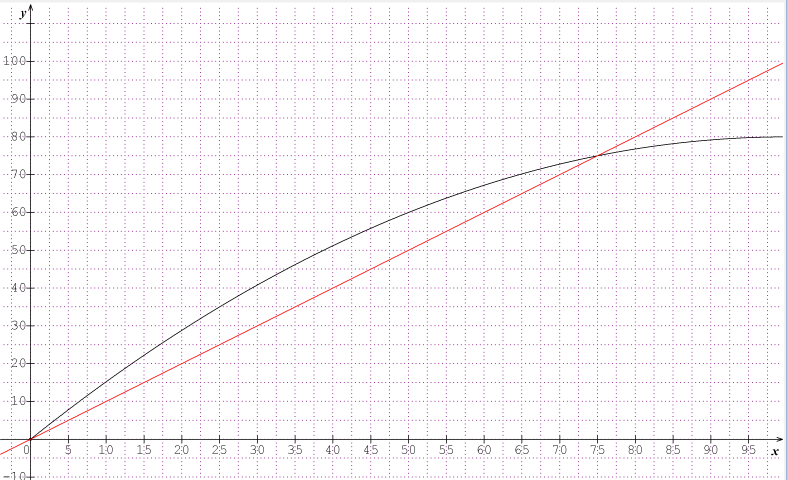
1-2-3 d'accord. Comme on peut le vérifier avec le graphique ci-dessous
Que veut dire
On admet que l =125.
Vous avez montré que la suite était croissante, majorée
vous avez montré que pour
La limite est unique. Désolé, je ne comprends pas la question.
D'accord avec hekla
Par ailleurs, il a été montré en 3) que tous les termes de la suite sont entre 0 et 100. alors comment la limite pourrait-elle être 125 ?
Erreur de frappe sans doute : 75 et non 125
à suivre
Et aussi , en 1) , le calcul donne bien 51,2 et est est sans doute à présenter.
Mais la réponse finale doit être un entier je pense : estimation d'un nombre d'oiseaux .... alors ?
Bonjour
Vous avez montré que la suite était croissante, majorée
vous avez montré que
La limite est unique. Désolé, je ne comprends pas la question.
Merci de votre aide je vais écrire que la limite est 75. Car dans mon cours il était écrit que la limite était solution de l'équation f(x) = x. Mais je ne comprenais pas pourquoi 125.
@co11
il n'y a pas de faute de frappe c'est bien 125 (mais c'est une question rajouter par mon professeur).
Pour l'estimation il y a donc 51 oiseaux
En tous cas merci pour vos réponses
1) Oui, pour l'estimation demandée) je répondrais 51 oiseaux effectivement.
Par ailleurs, dans ton premier message, question 3)d) , je lis :
On admet que l =125. Interpréter le résultat dans le contexte de l'exercice.
Vu les réponses reçues de la part de hekla et moi, que penses tu de cette question ?
Les maths ont aussi un aspect pratique
Bon à suivre s'il faut en dire davantage



