Inscription / Connexion Nouveau Sujet
suites graphiques...
Bonjour, voilà un problème sur les suites auquel je ne trouve guère de réponses, pourriez-vous m'aider:
Comment démontrer que le nombre de petits carrés utilisés pour construire une pyramide à n étages est égal à n2. En sachant qu'au premier étage, il y a 1 carré, au 2ème 3 carrés, au 3ème 5 carrés, au 4ème 7 carrés... etc.
Merci d'avance.
Il faut additionner les nombres impairs c'est à dire les termes d'une suite arithmétique de raison 2 et de premier terme 1.
Or la somme des termes d'une suite aithmétique est donnée par une formule de ton cours que tu peux appliquer maintenant 
Bonsoir,
Chaque étage est tel que un=un-1+2
On a affaire à une suite arithmétique de raison r=2 et de premier terme u1=1.
Donc un=u1+(n-1)r
Pour connaitre le nombre total de pavés de la pyramide , il faut additionner le nombre de chaque étage
Soit Sn=u1+u2+..+un
En remplaçant chaque terme ui par son expression, on obtient :
Sn=nu1+(r+2r+..+(n-1)r)
soit Sn=nu1+r*(1+2+..+(n-1))
càd puisque u1=1 et r=2:
Sn=n+2*((n-1)*n)/2)=n2
A toi de vérifier
Bonsoir,
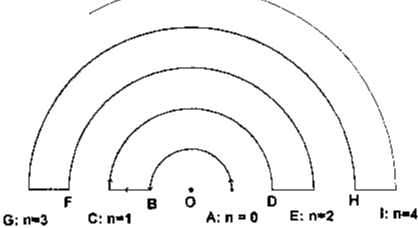
voici un autre problème concernant les suites, auquel je joinds une image pour mieux le comprendre (sur la figure, le signe entre n et le nombre est un égal)
OA=OB=AD=BC=DE=...=1 cm.
On parcourt une ligne faite de demi-cercles et de segments de longueurs 1 cm: le départ est en A et on s'arrête à C (pour n=1) ou E (pour n=2) ou...
On note Un la distance parcourue pour arriver au point au point correspondant à n.
1) Donner la valeur explicite de Un.
2) La suite (U) est-elle convergente?
3) A partir de quelle valeur de n distance parcourue est-elle supérieure à la distance entre la terre et le soleil.
Merci d'avance.
Bonjour,
Soit un la suite des chemins partiels et Unla suite pour aller du point A au point associé à n (soit Mn)
u0=0 et U0=0
Un est la somme des ui de i=0 jusqu'à i=n
Soit Un=u1+u2+...+un car u0=0
1) On voit tout de suite que le rayon d'un cercle de rang n vaut n (en cm) et le demi périmètre vaut donc n* (en cm)
(en cm)
Donc un chemin partiel vaut :
un=n* +1 (en cm)
+1 (en cm)
D'où Un=n+ (1+2+...+n)
(1+2+...+n)
Soit Un=n+ *n*(n+1)
*n*(n+1)
càd Un=n*(1+ *(n+1)) (en cm)
*(n+1)) (en cm)
2) Un ne converge pas puisque lim Un quand n tend vers + est +
est +
Tu apprendras plus tard que, pour qu'une somme (ou série) converge, il est nécessaire (mais pas siffisant) que ses composants tendent vers 0 (dans notre cas un doit tendre vers 0, ce qui n'est pas le cas).
Et on s'en rend très bien compte sur la figure
3) La distance Terre-Soleil d'après votre cours de Physique est de 150 *106 km.
Cette question est là à mon avis pour te confirmer que la suite Un ne converge pas.
A toi de vérifier et finaliser
A bientôt
Merci de m'avoir répondu, cependant je bloque sur un dernier problème, le voici:
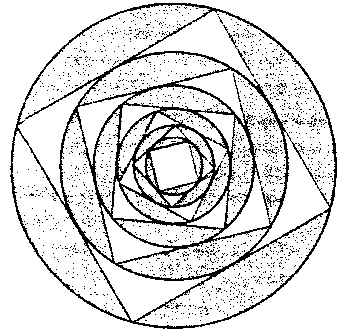
Un cercle de rayon 2 cm est donné. On construit un carré inscrit dans ce premier cercle, puis le cercle inscrit dans ce carré, et ainsi de suite. On suppose que ce programme de construction peut se poursuive indéfiniment. On veut étudier (monotonie et convergente) la suite des aires des disques et la suite des aires des carrés puis déterminer à partir de quelle étape l'aire du carré est inférieure à 1 mm². Notons dn l'aire en cm² du nième disque puis cn l'aire du nième carré.
1) Calculer d1, c1 puis d2 puis c2.
2) Prouver que dn+1=(1/2)dn et que cn+1=(1/2)cn. Qu'en conclure?
3) Le sens de variation et la convergence de ces deux suites sont clairement sugérées par la figure. Prouver que chacune des suites est effectivement strictement décroissante et converge vers 0.
Que dire de l'aire de la partie grisée? de celle de la partie blanche?
4) Déterminer l'indice n0 à partir duquel:
cn inférieur à 1/100.
Merci pour votre aide qui m'est très utile.
Bonjour Rom,
Es-tu sûr que tu n'es pas capable de faire cet exercice tout seul?
Commences déjà par faire un peu de géométrie
Soit R le rayon d'un cercle.
- Quelle est la surface d du disque de rayon R? soit d=f(R)
- Quelle est la valeur a du côté du carré inscrit dans ce cercle (Pythagore)? soit a=g(R)
- Quelle est la surface c du carré de côté a? soit c=h(a)=h(g(R))
- Quelle est la valeur du rayon R' inscrit dans ce carré? soit R'=k(a)=k(g(R))
Par la suite ces relations s'utilisent de la sorte :
dn=f(Rn)
an=g(Rn)
cn=h(an)
Rn+1=k(an)=k(g(Rn))
Un petit effort et tu devrais y arriver.
A+