Inscription / Connexion Nouveau Sujet
Tableau de variation
Bonsoir, alors voilà je vous explique mon problème :
Je bloque sur un résultat de mon devoir, la question est la suivante :
On considère la fonction f définie sur R par : x/x²+4 et on appelle C sa courbe représentative.
1) Calculer la dérivée de f puis dresser le tableau de variation de f.
J'ai trouvé le résultat suivant :
f'(x)= -x²+4/(x²+4)²
Est-ce le bon résultat ? Comment dois-je faire pour faire le tableau de variation à partir de celui-ci ?
Bonjour,
Le calcul de la dérivée est correcte. Pour le tableau de variation il faut étudier la signe du dérivée. Si la dérivée est positive alors la fonction est croissante. Si la dérivée est négative alors la fonction est décroissante. Si la dérivée est nulle alors la fonction est constante.
Oui je sais, il faut faire delta qui est b²-4ac. Mais mon résultat est une fraction, donc je ne sais pas comment m'y prendre, on m'a dit qu'il ne fallait pas tenir compte du dénominateur, mais je ne comprends pas :S
Bonsoir Cooralie
Ta dérivée est correcte ( prends l'habitude d'écrire les numérateurs et les dénominateurs avec des parenthèses lorsqu'ils comportent plus d'un terme
f(x) = x/(x²+4) f'(x)= (-x²+4)/(x²+4)² )
Ici , il faut étudier le signe de -x²+4
Ceci est un polynôme du second degré qui s'annule en 2 et en -2 , et son signe est celui du coefficient de x² ( négatif) à l'extérieur des racines , positif entre -2 et 2
Ainsi on peut faire le tableau suivant
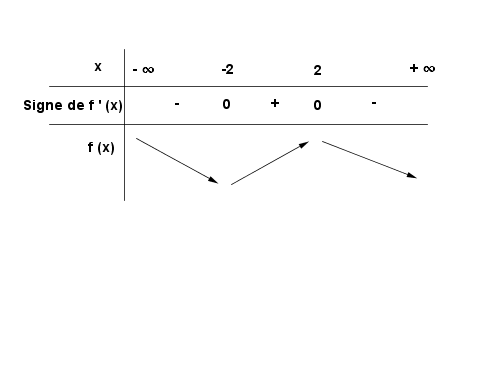
D'accord merci beaucoup Elisabeth67, mais pourriez-vous m'expliquer comment vous avec fait pour delta ? :S Car delta c'est b²-4ac, et dans -x²+4, je sais seulement que a=-1 et que c=4 et b ne peut pas être égale à 0 puisque ce serait impossible.
Si , b = 0 ici
Ainsi  = 0² - 4*(-1)*4 = 16
= 0² - 4*(-1)*4 = 16
Solutions : (-b+
 )/(2a) = 4/-2 = -2
)/(2a) = 4/-2 = -2
(-b-
 )/(2a) = -4/-2 = 2
)/(2a) = -4/-2 = 2
Ce qui était encore plus simple ici , c'est d'écrire -x²+4 sous la forme -(x²-4) = -(x+2)(x-2) ( 3ème identité remarquable )
Ah oui, je m'étais trompée dans mes calculs :S Mais en faisant une identitée remarquable, je n'aurais pas pu faire delta, donc je ne comprends pas pourquoi cela aurait été plus simple ?
Si on sait facilement factoriser , on a alors rapidement les valeurs qui annulent le polynôme , sans faire le delta



