Inscription / Connexion Nouveau Sujet
Tangente à une ellipse
Bonjour,j'ai un problème avec l'exercice suivant:
Dans le plan euclidien muni d'un repère orthonormé, on note  l'ellipse d'équation cartésienne réduite:
l'ellipse d'équation cartésienne réduite:
x2/a2+y2/b2=1
avec a>b>0. On note F(c,0) et F'(-c,0) ses foyers où c= (a2-b2). On appelle cercle directeur de l'ellipse le cercle de centre F' et de rayon 2a
(a2-b2). On appelle cercle directeur de l'ellipse le cercle de centre F' et de rayon 2a
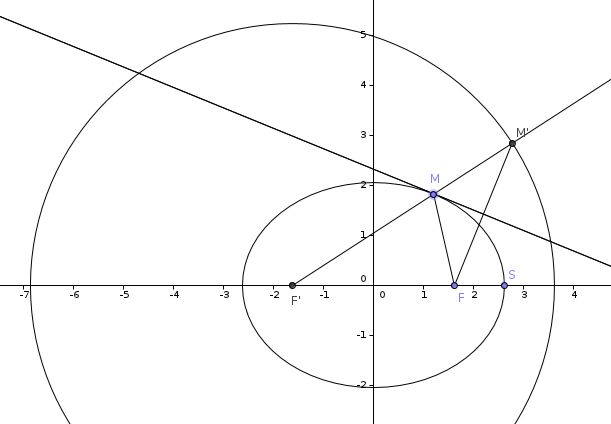
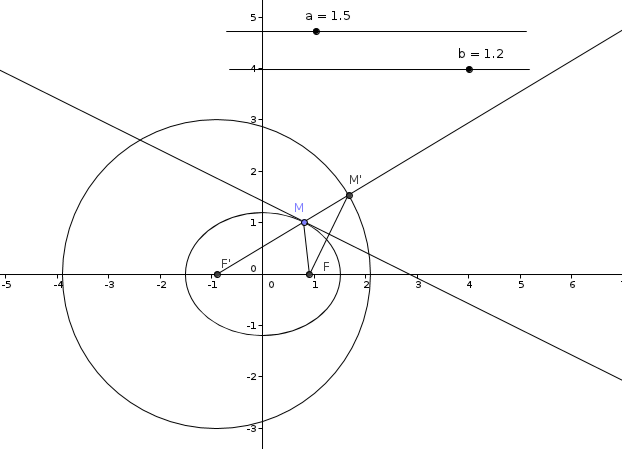
Soit un point M de l'ellipse. on note M' le point d'intersection de la demi-droite issue de F', dirigée par vecteur(F'M) et du cercle directeur. Montrer que la tangente en M à l'ellipse est la médiatrice du segment [M'F].
je ne sais pas du tout comment faire,j'ai essayé avec les équations des droites et des cercles mais les calculs étaient trop compliqués.Pouvez-vous m'aider
Merci d'avance
tu montres facilement que MF'=MM' : triangle isocèle, la médiatrice de FM' passe par M
puis tu calcules d'un coté la pente de la tangente (facile) et de l'autre celle de cette médiatrice
et tu conclues
Bonsoir
en suivant la piste de dhalte
encore un petit coup de pouce
|F'M'| = |F'M| + |MM'| = 2a et |F'M| + |MF| = 2a => |MM'| = |MF|
pente de la tangente en M(u;v) = -ub²/va²
il te reste la pente de la médiatrice qui est l'inverse et l'opposé de M'F
A+
Allez, encore une autre indication, que geo3 va s'empresser d'exploiter :
dans un triangle isocèle, la médiatrice est aussi bissectrice.
il te reste à calculer la pente des bissectrices
Le problème c'est que sans calculer les coordonnées de M',ce qui est trop compliqué, je ne vois pas comment trouver le coefficient directeur de la bissectrice de l'angle FMF'
bof, les calculs restent assez compliqués quand même
rappels :
ellipse centrée à l'origine O, de demi-grand axe de longueur a sur x'Ox, de demi-petit axe de longueur b
équation
soit c positif tel que c²=a²-b², F(c,0), F'(-c,0) sont ses foyers et pour tout point M de l'ellipse, F'M+FM=2a
soit le cercle de centre F', de rayon 2a, appelé cercle directeur de l'ellipse
Soit M' le point de obtenu par intersection avec la demie-droite [F'M)
Alors comme le soulignait geo3, F'M+MM' = 2a : c'est le rayon du cercle
F'M+FM = 2a : propriété de l'ellipse
donc FM=MM' et le triangle MM'F est isocèle de sommet M
la médiatrice de [FM'] passe donc par le sommet de ce triangle isocèle;
reste à montrer que sa pente est égale à celle de la tangente. Pour cela, je me propose de calculer la pente de la droite (FM') perpendiculaire à cette médiatrice. Si le produit de la pente de la tangente et de celle de cette droite font -1, alors elles sont perpendiculaires et la tangente et la médiatrice sont parallèles, et puisqu'elles passent toutes deux par M, elles seront confondues.
un simple calcul différentiel montre que la pente de la tangente est (en dehors des sommets du grand axe, où la pente est infinie, mais la médiatrice est elle-même trivialement verticale)
Cherchons maintenant la pente p de (FM')
soit M(x,y) point de l'ellipse et M'(x',y') point du cercle directeur associé
(x,y) vérifie
(x',y') vérifie
pour calculer x', on peut faire la remarque suivante :
grâce à Thalès, nous avons
et on veut calculer la pente p qui est égale à
nous remarquons que
et
donc
le problème est symétrique par rapport à x'Ox, donc nous pouvons travailler avec y>0 et donc y'>0
calculons et
donc
donc
nous en déduisons
suite aux remarques sur les signes qui précèdent, nous établissons, pour x>c comme pour x<c
suite à la remarque sur le signe de y et y'
on remplace x'-c et x'+c par les quantités trouvées,on utilise abondamment et aussi
et voilà
Bonjour
-> dhalte
bravo à toi
sorry l'autre jour pour le manquement de parenthèses
hier j'avais essayé pour la pente de la médiatrice ( ou bissectrice) de la chercher par les angles mais comme pour la bissectrice on devait avoir tan[( +
+ )/2] connaissant tan(
)/2] connaissant tan( ) et tan(
) et tan( ) il me fallait tan(
) il me fallait tan( /2) en fonction de tan(
/2) en fonction de tan( ) ce qui rationnellement n'était pas possible
) ce qui rationnellement n'était pas possible
alors j'avais abandonné
J'allais chercher la pente de FM' mais voyant ta démonstration à mon avis je n'aurais pas trouvé dans un temps raisonnable.
Félicitations


 géométrie en post-bac
géométrie en post-bac