Inscription / Connexion Nouveau Sujet
tangente, limites derivés exercice 1ère S non compris
bonjour
j'ai un exercice a terminer pour cause d'un DS très important mercredi mais je bloque sur la dernière question
j'ai une fonction : f(x) = 2x-1/2-x
j'ai du montrer que la fonction était dérivable en -2, cela donnait 3/16
j'ai du donner l'équation de la tangente T au point d'abcisse -2, cela donnait y = 3/16x-7/8
j'ai étudié les positions relatives de Cf - y
et la dernière question était : on admet pour tout a appartenant a R - (2), f'(a) = 3/(2-a)²
on note delta la droite d'équation y=3x+4
determiner les points de Cf ayant une tangente parallèle à delta
j'ai juste compris pour qu'elles soit parellèles, il faut que leurs coefficients directeurs soient égaux mais je ne sais pas comment le démontrer
merci d'avance
Bonjour,
La fonction que tu dois étudiée (celle donnée par l'énoncé) n'est sûrement pas celle que tu as écrite ici....
Consulte le lien suivant
![]() [lien]
[lien]
Cela est très important surtout quand tu vas essayer de saisir ce type de fonctions dans ta calculatrice qui elle est très rigoureuse 
oh pardon ZEDMAT du coup la fonction est f(x) = (2x-1)/(2-x)
et le coefficient directeur de la tangente je pense que c'est f'(x) = 3/(2-a)
tu as perdu le carré au dénominateur, et ce n'est pas f'(x) mais f'(a)
eh bien écris que f'(a)=3
et tu vas trouver a
Quand tu auras trouvé la (ou les) valeur(s) de a, tu pourras vérifier graphiquement 
(figure faite avec GEOGEBRA)
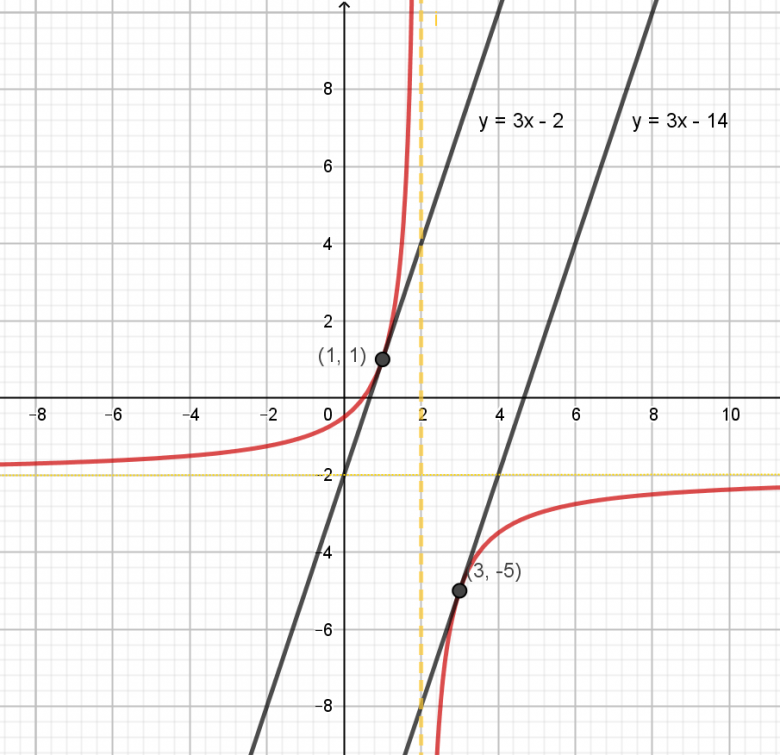
oui j'ai mal appuyé sur les touches
c'est bien f'(a) = 3/(2-a)²
il y a bien un carré
mais je ne comprends pas pourquoi cela doit être égal à 3 malou
merci pour vos réponses
"mais je ne comprends pas pourquoi cela doit être égal à 3 "
Es tu bien d'accord que si 2 droites sont parallèles, elles ont le MEME coefficient directeur ?
Pour la tangente c'est, au point cherché d'abscisse a, le nombre f'(a) et pour la droite "delta " d'équation y=3x+4, c'est ... 3.
On cherche le nombre a (abscisse du point de tangence) pour lequel on a f'(a) = 3.
merci beaucoup pour vos réponses rapides
j'ai compris et j'ai fais l'exercice
je l'ai donné à la prof qui m'as confirmé que c'etait bon
encore merci



