Inscription / Connexion Nouveau Sujet
thales
bonjours voici le schma et l'enoncer
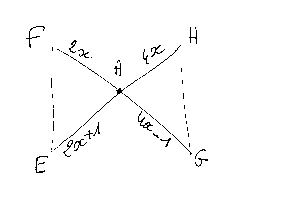
les droites (ef) et (gh) sont paralleles
calculer x en utilisant les informations de la figure (donner en cm)merci j'ai utiliser le theoreme de thales mais je suis ploquer avec les x pouvez vous m'aider
Rebonjour 
Théorème de thalès : produit en croix 
4x (4x-1) /2x =2x+1
(16x2 - 4x )/2x = 2x + 1
8x -2 = 2x + 1
8x = 2x + 3
6x = 3
x = 1/2
bonjours je seche le theoreme de thales ah/ae =ag/af
je ne conprend pas pourquoi on divise part 2x et comment vous trouver 8x
Ils me disent que c trop gros pas grave je vais essayer d'écrire
2x/4x-1=2x+1/4x
On supprime la fraction de droite :
8x2 / (4x-1) = 2x +1
8x2/4x-1 = 2x+1
8x 2 = 8x2 + 2x -1
(On a supprimé la fraction à gauche)
8x2-8x2 = 8x2-8x2 + 2x-1
0 = 2x-1
2x = 1
x = 1/2
Voilà  good luck ^^
good luck ^^
Bonjour alors j'ai exactement le même sujet et je suis bloquer au x , je n'ai pas compris elles explications est ce que ce serait possible que vous ré expliquer s'il vous plaît
*****
correct aurait du être à la rigueur
que ne comprends tu pas dans cette réponse
(modération)
Bonjour,
![]() à LIRE AVANT de répondre, merci
à LIRE AVANT de répondre, merci
et de toute façon : avec de telles explications c'est normal qu'on ne comprenne pas
écritures mauvaises
2x/4x-1=2x+1/4x est faux dès le départ ce qui est écrit veut réellement dire
ou à la grande rigueur en inventant une multiplication implicite plus prioritaire que la multiplication explicite
et que la division
à cause de la priorité de l'opération de division "/"
qui ne veut absolument pas dire "barre de fraction" (quelle en serait la longueur ???) s'écrit 2x/(4x-1) = (2x+1)/(4x) parenthèses ajoutées absolument obligatoires
fautes de frappes
explications insuffisantes mais tant mieux.
pilote / pilote20 ... ??



