Inscription / Connexion Nouveau Sujet
Thales
Bonjour pouvez-vous m aider pour cet exercice merci
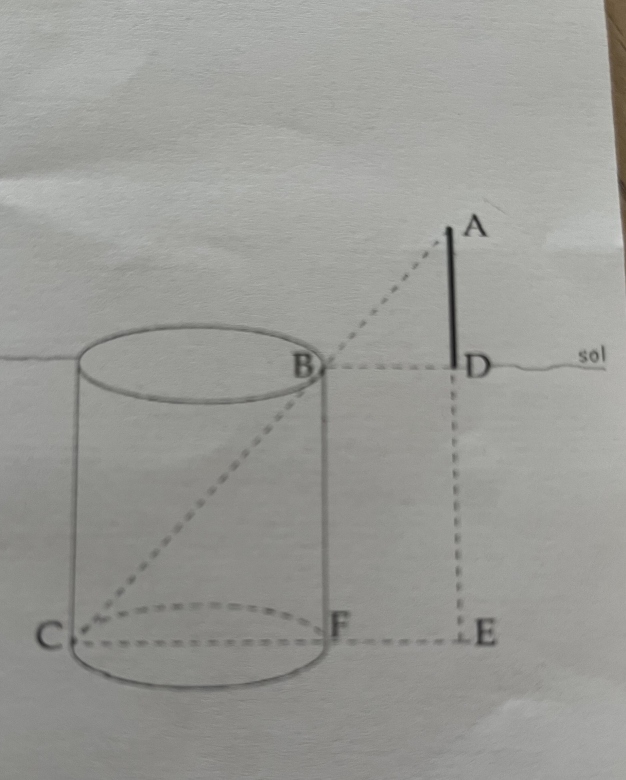
On souhaite mesurer la profondeur d'un puits vide de 2 m de diamètre et dont les parois sont bien verticales. Pour ce faire, on plante verticalement un bâton de façon que le sommet A situé à1,5 m du sol, le point B au bord et le coin C au fond du puits soient alignés
Voir figure ci-contre
De plus, la distance entre le pied et du bâton D. Et le bord du puits B est égal à 0,5 m.
Calcule la profondeur de ce puits
Re
c'est une application directe du théorème de Thalès
vous connaissez:
|AE|= 1.5 m
|CF|=2 m
|FE|=0.5 m
et on vous demande |BF|
Voilà ce que j ai fait
AB/AD=BC/BD
On sait que AD est égal à 1,5 m
On sait que BDest égal à 0,5 m
Donc
1,5/0,5=h/0,5
3=h/0,5
h=3x0,5 =1,5 m
La profondeur du puits est de 1,5 m
Pouvez-Vous me corriger merci
Je arriver pas a trouver la bonne formule car il me manque pleins de chiffres je ne dois pas prendre les 2 bons triangles pour calculer
Donc si je fais
AB/AC=AD/AE=BD/CE
1,5/AE=0,5/2,5
AE=1,5x2,5/0,5
AR= 7,5 m
7,5-1,5 =6
La profondeur est de 6 m
AR=7.5 m? AE=7.5m
on écrira plutôt d'où m
remarque, on pouvait trouver directement en écrivant que
d'où on tire
Annuler
connectez vous