Inscription / Connexion Nouveau Sujet
theoreme de pythagore
voici mon exercice:
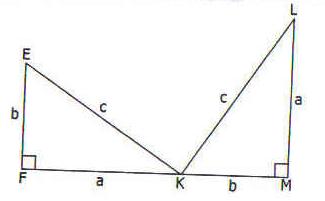
La figure ci -contre est constituer de deux triangle respectivement en f et m . Les points f k m sont alignes.
a)Demontrer que EKL est un angle droit.
Voici ma reponse:
Le triangle EFK est rectangle en f .L'hypothenuse est [EK].La somme des carres des cotes de l'angle droit est EF2 +KF2
J'ecrit la relation de pythagore:
EK2=EF2+KF2.
Est ce que j'ai bon merci.
bonjour a toi
oui tu as presque bon sauf qu il faut que tu dises "la sommes des 2 cotés opposés à l hypotenuse est egale à la somme de l hypothenuse au carré" sinon le reste est bon
allez bonne chance
a+
ps: ne t inquiete pas pour mon pseudo je suis en 2nde mais en 4 eme j y arrivais
et j'en ai encore
b)Ecrire en fonction de a b c l'aire des triangle EFK ,KLM et EKL en recopiant et en completant le tableau suivant:
voici le tableau:

c)Demontrer que les droites (EF)et(LM) sont parralleles
d)Calculer l'aire de EFML de deux façon differentes.
Indication:vous pourrez utiliser la relation(a+b)(a+b)=a2+2ab+b2
e)Conclure.
merci de votre aide
qui peut m'aider la dessus car je n'arrive pas a finir cette exercice merci je suis dessus depuit ce matin
salut,j'ai le même éxercice a faire si tu a les corriger parce-que je l'ai fait mais pas trop sur de ce que j'ai fait merci de répondre
bonsoir,
a)Demontrer que EKL est un angle droit.
les 2 triangles ont les mêmes longueurs de côtés , ils sont superposables
donc (les angles) FEK = LKM or FEK + FKE = 90°
donc on peut calculer EKL
b)Ecrire en fonction de a b c l'aire des triangle EFK ,KLM et EKL
aire du triangle = (base  hauteur) /2
hauteur) /2
or dans le triangle rectangle les 2 côtés de l'angle droit peuvent servir de base et de hauteur
c) Demontrer que les droites (EF)et(LM) sont parallèles
facile... : 2 perpendiculaires à la même 3ème .....
d) Calculer l'aire de EFML de deux façon différentes.
1. en additionnant les aires des 3 triangles
2. quelle est la nature de EFML? il existe un formule d'aire (fin du livre ou certains cahiers de texte)
eh,bien comme formule(nature)j'ai mis sa:Théorème de Pythagore — Dans un triangle rectangle, le carré de la longueur de l'hypoténuse (côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des côtés de l'angle droit.
Il me manque plus que la question : d) Calculer l'aire de EFML , de deux façon différentes.
e) Conclure.
(Je ne comprend rien aider moi svp).
bonjour,
A(EFML)=A(EFK)+A(KML)+A(EKL)
= ab/2 +ab/2 +c²/2
=2ab/2 + c²/2
=c²/2 +ab
A(trapèze)=(grade base+ petite base)*hauteur/2
A(EFML)=(EF+LM)*FM/2
=(a+b)(a+b)/2
=(a+b)²/2
=(a²+2ab+b²)/2
=(a²+b²)/2 +ab
or a²+b²=c²
--->=c²/2+ ab
c=puisque les droite (ef) et (lm) sont toute deux perpendiculaires a la droite (fm) alors elle sont parallèles entre elles
nature=
théorème de pythagore=Dans un triangle rectangle,le carré de la longueur de l'hypoténuse (coté opposé a l'angle droit) est égal a la somme des carrés des longueurs des cotés de l'angle droit.
Ce sont 2 triangle rectangles,c'est un parallélogramme.
d=aire de efk+aire de mlk
=ab/2 + ac/2
=ab+ac/2
=2ab+c/2 ;
sinnon,ab*ba = ab au carré
e= 1) En additionnant les aires des 3 triangles
2) voir petit a
voila 20/20 Mdr j'éspère que tu va réussir a écrir tt sa