Inscription / Connexion Nouveau Sujet
théorème de Pythagore
Bonjour,
Je bloque sur cet exercice : "Des élèves font un cross dans un parc. Combien de tours du circuit ABCDA doivent-ils faire pour parcourir 1,8km ? Sur quels points s'arreteront-ils ?" Je pense qu'il faut utiliser le théorème de Pythagore, mais dans les triangles rectangles que je vois dans la figure, on ne connait la longueur que d'un seul coté. Comment puis-je faire ? Merci d'avance car je ne sais pas du tout comment faire.
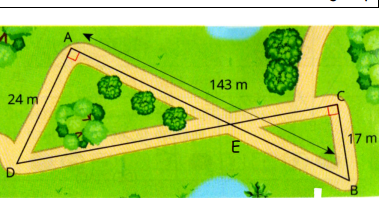
ET si tu considérais le triangle rectangle ADB rectangle en A
puis, dans un deuxième temps, le triangle rectangle DCB rectangle en C
Bonjour,
En effet tu peux utiliser Pythagore pour résoudre ce problème (puisque la question repose notamment sur le fait de connaitre toutes les distances du parcours).
Regarde bien les données dont tu dispose:
On te dit de calculer le parcours ABCDA, mais ne disposes-tu pas d'autres informations dans l'énoncé ?
Pas de quoi, pour la question 2°, le plus simple selon moi est d'additionner les tours jusqu'a arriver proche de 1,8km puis de faire de segments en segments, cependant il faut supposer que les coureurs commencent au point (A) par exemple.
Bon courage!
Bonjour,
"le circuit ABCDA" se parcourt en partant de A puis B puis C etc ...
donc aucune ambiguïté sur le point de départ.
oui , je pense avoir trouvé la solution. On doit faire 5 tours du parcours en partant de A et il reste 150 m à faire pour avoir une distance de 1,8 km . En s'arrêtant au point B, il manque 4 mètres mais je ne vois pas comment obtenir précisément 1,8 km
montres le détail.
parce que c'est faux.
base des bases des calculs :
ne jamais arrondir quoi que ce soit dans les calculs
mieux : faire les calculs entièrement en littéral jusqu'au bout du bout
et seulement tout à la fin remplacer par des valeurs numériques.
Bonsoir
On arrondi CD à 146 m
Tu as trouvé le parcours mesure bien 330 m.
1800 / 330 ne donnant pas un nombre entier de tours ,
Tu gardes 5 soit 5x330 = 1650
et 1800-1650 =150 m après le point A
Le point B est onc dépassé de:
150-143 = 7 m
mathafou va me gronder car j'ai dit exactement le contraire,
donc tu vas faire comme il dit avec 145.993151 m et autant de décimales
que tu voudras ..........
ou tout en littéral pour trouver à la fin :
et trouver que la valeur exacte de CD est exactement un nombre entier sans faire aucun arrondi du tout vu que arrondir un nombre déja entier ça n'a pas de sens...
Oui , j'ai trouvé les mêmes chiffres que dpi ( je me suis trompé, c bien 7 m qui restent après avoir fait 5 tours).
J'ai arrondi la racine de 21314 à 146m pour la longueur de CD
si on fait comme je viens de dire il n'y a aucun arrondi à faire vu qu'il n'y a partout que des nombres entiers ...
(et à la fin on atterrit exactement sur le point C)
Merci Mathafou. je trouve exactement le point où les coureurs s'arrêteront après avoir fait 1800m . Je retiens la leçon : ne pas arrondir dans les calculs
>mathafou
Je suis désolé d'avoir fourché 
CD n'est pas une hypoténuse mais un grand coté
et mesure exactement 144 m.
flovic ayant compris le raisonnement va donc rectifier..



