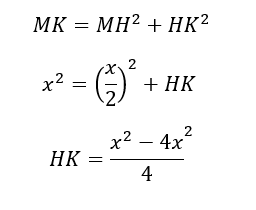bonjour

" CM et KH sont égaux "   ?

je ne sais pas comment je dois proceder pour trouver AM
l'énoncé exact nous dira peut-être que AM=x

...tu nous racontes l'énoncé, mais il est préférable que tu le recopies exactement et entièrement tel qu'il est donné.

bonjour l'enonicer dit Un triangle ABC rectangle en A est tel que : 𝐴𝐵 = 8 𝑐𝑚 et 𝐴𝐶 = 4 𝑐𝑚.

M est un point variable du segment [AB] et on
pose 𝐴𝑀 = 𝑥cm. On considère le triangle équilatéral MBK
de hauteur [KH], avec K et C de part et d'autre de la droite
(AB). On souhaite montrer qu'il existe une position de M
telle que 𝐶𝑀 = 𝐾𝐻et préciser si, dans cette position, les
points C, M et K sont alignés ou pas.
(Utiliser le théorème de Pythagore):

1- Calculer 𝐶𝑀2 dans le triangle ACM
2- Calculer 𝐾𝐻
2 dans le triangle KHM
3- Trouver l'équation avec :𝐶𝑀2 = 𝐾𝐻
2 et résoudre
4- Pour l'alignement des points : travailler tel que l'angle
𝐶 𝑀𝐴 = 𝐵 𝑀𝐾 = 60° (angles opposés par le sommet

1- Calculer CM² dans le triangle ACM

Pythagore, oui, pour trouver CM²  (CM est l'hypoténuse du triangle ACM)

avec AC = ...?  et     AM = ....?     d'après l'énoncé

montre ce que tu as fait ensuite

---
2- Calculer KH²   dans le triangle KHM
la question incite aussi à utiliser le théorème de Pythagore pour exprimer KH² en fonction de x

on sait que MK = MB = ....?    
donc MH = ...?

à toi
montre le détail de tes calculs si tu as des difficultés.  

bonjour pour la question 1

pour l'nstant j'ai utiser pythagore pour le triangle  ABC pour trouver la longuer de l'hypotenus CB=8,94cm  et  j'ai aussi trouver l'ongle ACB=63° ET ABC= 27°  j'ai fais ça pour essayer de trouver une solution.  

et j'ai aussi j'ai écrit ça : AM=AB-x
mais ça ne marche pas.  Et je sais que tant que j'ai pastrouver AM je ne peux pas appliquer le théoreme de pythagore

mais je n'arrive toujours pas à faire le liens ou trouver une solution pour le triangle ACM.

calculer CB ne te servira à rien ici, pas plus que les angles du triangle ABC

AM=AB-x    ---- ceci est faux

==> l'énoncé dit AM = x : c'est posé dès le départ !
dans la formule d'application de Pythagore, tu remplaces AM par x, tout simplement.

et bien évidement, CM² sera exprimé en fonction de x.

question : à ton avis, à quel intervalle appartient x ?

Bonjour j'ai trouvée ça j'espère que c'est bon

Aussi pour l'intervalle je ne sais pas pouvez vous m'expliquer?

les photos de brouillon sont interdites sur le site : tu dois taper tes réponses au clavier.

révise le théorème de Pythagore (et les propriétés de la racine carrée!) :

CM² = AM² + AC²
CM² = x² + 4² = .... ?         ------   4² n'est pas égal à 8

l'énoncé demande CM², donc inutile de prendre la racine carrée du résultat.

---

à quel intervalle appartient x ?
quelle est la plus petite valeur possible que peut prendre  x ?
la plus grande valeur possible ?
donc x [..... ; ......]  ?

aide toi du dessin pour répondre à ces questions.
elles ne sont posées explicitement, mais à la question3), cet intervalle te sera utile.

BOJOUR POUR HK j'ai trover ça est ce que c'est bon ou pas

CM²=16 +x²

L'intervalle  [x]appartient [4;16]

je ne comprend pas la question 4 et je n'arrive pas à faire la question 3 vous povez m'aider svp mercie

bonjour

27-12-21 à 21:55
tu refais la même erreur que précédemment : tu oublies des "carrés" dans l'égalité de Pythagore.
corrige-la

l'autre erreur provient du fait que MH n'est pas égal x/2
regarde le dessin :
AB = 8
AM = x

or AB = AM + MB
donc MB = ....?

puis MH = MB/2 = ...?

---

27-12-21 à 21:58                 CM² = x² + 16       exact

---

27-12-21 à 22:14     non

énoncé : M est un point variable du segment [AB] et on pose 𝐴𝑀 = 𝑥 cm.
AM = x  est la distance en cm , entre les points A et M

>> si M est confondu avec le point A  (i.e. si M est sur A), alors la distance AM = ..?
donc la valeur minimale de x est  ...?

>> si M est confondu avec le point B  (i.e. si M est sur B), alors ... continue

d'où x [... ; ... ]

---

3- posez l'équation CM² = KH²    et résoudre

CM² en fonction de x, tu as trouvé en 1)
KH² tu vas trouver en 2)
restera à poser l'égalité entre les 2 expressions, et résoudre.

Bonjour,
@Mahum,
Attention, deux images non autorisées dans ce sujet, ça fait beaucoup
Tu as vu ceci chaque fois que tu as posté une image :

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

bonjour est ce que
AB²=AM²+MB²
8²=x²+MB²
MB²= 8²-x²
donc
MH = 8²- x²/2²

Mahum, on ne peut appliquer le théorème de Pythagore que sur un triangle rectangle.

quand tu écris AB²=AM²+MB², cela signifie que le triangle AMB est rectangle en B...
on n'est d'accord que c'est totalement faux !

MB, c'est la distance entre M et B
si AM = x et  AB = 8, alors MB = ...?     ---- une simple soustraction suffit.

puis MH = MB/2  ceci est juste
puisque la hauteur issue de K est aussi la médiane issue de K (MBK est un triangle équilatéral);
le point H est donc le milieu du segment [MB]

oups, je rectifie
* quand tu écris AB²=AM²+MB², cela signifie que le triangle AMB est rectangle en M   (et non en B)

et aussi est ce que je dois enlever les carrés ou pas?
Et pour l'intervalle j'ai trouver [0;8]

et aussi est ce que je dois enlever les carrés ou pas?  bien sur

MB = 8 - x

juste un exemple pour clarifier :
si M est à 3 cm de A, c'est-à-dire si x = 3
alors la distance entre M et B est :  MB = 8-3 = 5 cm
d'accord ?


Et pour l'intervalle j'ai trouver [0;8]  bravo!
résultat à garder sous le coude, pour mémoire

mercie
du coup pour le triangle MHK la formule c'est ça ou pas

MK²=MH²+HK²
X²=(8-x/2)²+HK²
HK²=(8-x/2)²-x²

si cet formule est bonne je dois faire une egalité entre la formule de la question 1 ET 2 ET résourdre l'equation?

tu as fait 2 erreurs  :

MK²=MH²+HK²      oui
X²=((8-x)/2)²+HK²    -----  MK n'est pas égal à x

==> regarde le dessin : MBK est équilatéral
donc MK = ...?


HK²= (8-x/2)²-x²    ---- ici, tu fais des erreurs de signe

on a MK²=MH²+HK²  
donc HK²   =  MK²  - MH²

reprends
---

je dois faire une egalité entre la formule de la question 1 ET 2 ET résourdre l'equation?
oui
montre le détail de tes calculs si tu as des difficultés

MK=MB=BK
donc
MK = 8-x

HK²=[(8-x)/2]²-(8-x)²
CM=x+16
ET JE FAIS L'égaliter

le x est au carré j'ai ublier de le mettre

MK=MB=BK   oui
donc
MK = 8-x    oui

à partir de là, corrige ce que tu as fait à 14h21 pour trouver HK²
n'oublie pas d'écrire (8-x)/2 avec des parenthèses, sinon, ce sera faux.

HK²=[(8-x)/2]²-(8-x)²   --- non tu te trompes encore dans les signes

MK² = HM² + HK²
HK² =  MK² -  HM²    
donc
HK²=  (8-x)²  -  [(8-x)/2]²       et pas l'opposé
à noter que tu peux simplifier cette écriture ici... cela te simplifiera l'équation de la 3)

---

CM²=x²+16   oui

l'équation à résoudre est donc   CM² = HK²

à toi

CM²=KH² pour ça j'ai trover 2 résultats est ce que l'un des 2 est juste
x²+63/4 ET 5x²/4+16-x est ce que l'un des 2 est bon?

OU BIEN CM² = HK² ca donne ça
x²+16

non, là tu t'égares

commence par simplifier ceci :   HK²=  (8-x)²  -  [(8-x)/2]²   = ......?

je t'aide pour le début

mets sur dénominateur commun...

bonjour est ce que KH²  = 1

OU KH= 192-44x-3x²  

est quetoute l'égaliter donne ça
: -2x²  -176+44x=0

l'équation CM² = HK², après simplification, est équivalente à
x² + 48x - 128 = 0  ----   tu dois arriver à ça

puis résoudre (il s'agit d'une équation du second degré)

montre le détail de tes calculs si difficultés

ps : les messages de 18h24 et 18h29 sont farfelus

Apres avoir resolue l'équation
j'ai trover 2 solution 2,53 ET -50,53

oui environ, tu y es

maintenant, regarde l'intervalle auquel appartient x   ( 28-12-21 à 14:04)

qu'en déduis-tu ?

est ce que vous pouvez m'expliquer la question
4 - Pour l'alignement des points : travailler tel que l'angle
𝐶 𝑀𝐴 = 𝐵 𝑀𝐾 = 60° (angles opposés par le sommet)

je ne suis pas sûr je pense que vu que 2 appartient à l'intervalle [0;4] ca veut dire qu AM = 2 cm

dernière question :
On souhaite montrer ...  si, dans cette position, les
points C, M et K sont alignés ou pas.

4- Pour l'alignement des points : travailler tel que l'angle
𝐶 𝑀𝐴 = 𝐵 𝑀𝐾 = 60° (angles opposés par le sommet)

explique rapidement pourquoi

si les points sont alignés, alors on doit trouver que l'angle

==> tu dois donc calculer cet angle avant de conclure : utilise la trigonométrie
je te conseille d'utiliser la valeur exacte de la solution que tu as trouvée en 3), pas une valeur approchée.

je te laisse réfléchir à cette question 4)
et reviendrai te lire demain.
bonne soirée

\widehat{BMK} = 60°  Car c'est un triangle équilateral donc chaque angles vaut 60° et que la somme des angles d'un triangle dois être égale à 180°

EST ce que pour la question de déduction de l'intervalle j'ai bon?

Bonjour j'ai refais plusieurs fois mais je ne comprends pas où je me trompe

** image supprimée **

A chaque je refais en assayant de changer l'ordre d'operation mais je ne trouve jamais la valeurs que vous avez donnée

et sur certaine je trouve une solution égale à 2 ou 4 et  je ne sais pas  la laquelle est la  bonne

@Mahum,
Tu n'as pas tenu compte de mon message de 12h17.

extrait de la FAQ du forum :

Q30 - J'ai été averti ou banni, pourquoi, et que faire ?

J'ai été averti ou banni parce que je n'ai pas respecté les règles du forum, qui étaient à lire avant de poster. et donc acceptées tacitement lors de l'inscription.

Ou bien j'ai un triangle rouge devant mon pseudo et je suis averti. Je peux réagir dès que je le désire, en m'engageant à respecter le règlement (une phrase à recopier), et je peux lever mon avertissement moi-même. Pour cela, je tente de répondre à mon message, et la procédure apparaît.
Un conseil cependant : vraiment lire le message "A lire avant de poster" et ne pas récidiver...Vous seriez alors banni.

Si je suis averti pour ne pas avoir respecté la manière de poster expliquée en Q05 , je relis Q05 , puis je lève mon avertissement et je reposte mon énoncé correctement cette fois, dans le même sujet, et ainsi j'obtiendrai de l'aide rapidement très certainement.

Ou bien ma figurine est masquée, j'ai été banni pour un certain temps, et je dois en attendre la fin.

Mahum, tu vas te faire remonter les bretelles par la modération qui t'a déjà prévenue à 12h17 :
les photos de brouillon sont interdites

... recopie rapido-presto ce qu'il y a sur ton brouillon, il va être supprimé,
et je n'ai pas le droit d'y répondre tant que ce ne sera pas fait :
même les aidants doivent se plier au règlement.

ps : quitte à recopier, vérifie tes erreurs de signes...
je confirme que l'équation réduite à établir est x² + 48x - 128 = 0,
et que  les solutions à trouver sont  2,53 et -50,53 (en valeurs arrondies).
à demain !

ah ben voilà !

bonjour est ce que vous pouvez m'expliquer comment vous êtes arriver a trouver cet équation x² + 48x - 128  parce que moi je trouves des résultas differents du votre? moi j'ai trover  x² + 12x - 32