bonjour,
Je dois résoudre le problème suivant.
Dans l'antiquité, lorsqu'un arpenteur voulait mesurer la profondeur d'un puits dont il connaissait le diamètre, il alignait son oeil avec le bord du puits et le point opposé du fond du puits.
Connaissant la distance de recul de l'arpenteur par rapport au bord du puits et la distance entre l'oeil et les pieds de l'arpenteur, on pouvait en déduire la profondeur du puits.
Théo décide d'employer cette méthode pour mesurer la hauteur d'un puits dont le diamètre est de 1,20  m, il se place à 1 m environ du bord et aligne son oeil à 1,50 m  de hauteur avec le bord de celui-ci et le coin opposé du fonds du puits.
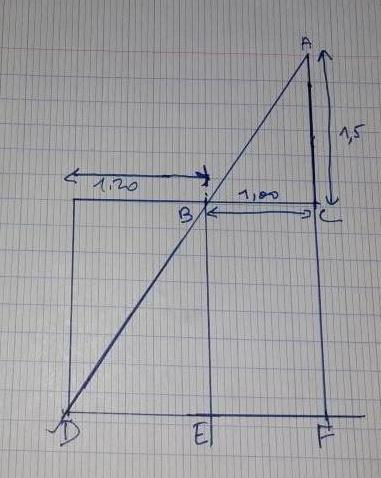
Après avoir fait le schéma, en, déduire la profondeur du puits.
Pour répondre à cette question, j'ai  utilisé le théorème de Pythagore et le celui de Thalès.
J'ai donc d'abord tracé un nouveau  triangle rectangle de sommet A  AFD  rectangle en A.
Il y a donc 4 triangles rectangles que nous pouvons utiliser pour répondre à la question : AFD rectangle en A ; ACB rectangle en C, BED rectangle en E et BGD rectangle en G .
Le triangle AFD et le triangle ACB dont les côtés BC et DF sont parallèles car perpendiculaires à AF. On peut dire que ABC est l'image de ADF par homothétie de centre A.
J'ai d'abord calculé l'hypoténuse AB du triangle ACB :
AB²=AC²+CB
AB<sup>[/sup]=1,5
J'ai ensuite appliqué le théorème de Thalès pour calculé BD
AB/AD=AC/AF=BC/DF
BC/DF = 1/2,20
AC/AF = 1,5/AF
AF = 3,3

AD[sup]2</sup>-AB^{[/sup]=BD[sup]2}
3,3²+2,2²=15,73-1,5=14,25
BD ²=1,2²+BE²
14,75-1,44 = 13,31
BE= = 3,65 mètres

La profondeur du puits est de 3,65 mètres