Inscription / Connexion Nouveau Sujet
théorème sur les triangle rectangle et cercle circonscrit
Bonjour, voila j'ai un devoir maison de maths a rendre pour le 10 mars, je suis en classe de 4ème.
voila j'ai un devoir maison de maths a rendre pour le 10 mars, je suis en classe de 4ème.
j'aimerai un éclaircissement de votre part sur cette exercice :
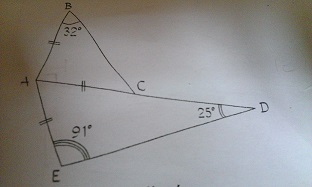
Ludo a dessiné cette figure a main levée.
Voir image en fin.
1) Montrer que les points B, A et E sont alignés.
2)Qu'en déduit-on pour le triangle BCE ? Justifier la réponse.
voila mon hypothèse mais je ne suit pas vraiment sur de moi :
1) j'ai tracer le cercle circonscrit a ABC que je nome (C)
On sait que : AB est un diamètre du cercle circonscrit
Or : si un triangle est inscrit dans un cercle dont un diamètre est un coté de ce triangle alors il est rectangle. L'hypoténuse du triangle est le diamètre du cercle.
Donc : Le triangle ABC est rectangle. (l'angle BAC mesure donc 90 degrés.)
Je pourrai donc ensuite utiliser le théorème des angle opposée mais je ne suis pas sur de ma première démonstrations est elle valable ?
Merci d'avance 
Bonjour,
1) Si les points A, B et E sont alignés alors (angle plat).
2) Que représente (AC) pour le triangle BCE?
Bonjour
As-tu remarqué que le triangle ABC est isocèle en A car AB=AC
Si ABC vaut 32°, combien vaut ACB ? et BAC ? sachant que la somme des 3 angles d'un triangle vaut 180°
de même dans le triangle AED, que vaut l'angle EAD ?
et la somme de BAC et de EAD vaut combien ? ce qui te permettrait de répondre à la question 1)
Tu dois être en mesure de répondre à la question 2)
D'accord donc Pour le triangle AED l'angle EAD est donc égale a 64°?
si les angles EAD et BAC sont opposés alors il sont égaux BAC=64° ?
Donc si ABC vaut 32° alors je fais 180-(32+64)=84°?
l'angle ACB mesure donc 84°?
mais 64+64 ne font pas 180° sa ne fait donc pas un angle plat alors les points ne sont pas alignée ? 
Bonsoir,
Quelle est la mesure de l'angle A dans le triangle ABC ?
Quelle est la mesure de l'angle A dans le triangle ADE ?
Quelle est la mesure de l'angle A formé par ces deux angles ?
Merci pour t'on éclaircissement
Voila ce que j'ai fait :
Ont sait que:
-AED=91°
-EDA=25°
Or: la somme des angles d'un triangle est égale a 80°
d'ou: 180-(91+25)= 64
Donc: EAD=64°
On sait que:
-EAD=64°
-Les angles EAD et BAC sont opposés
Or: Si deux angles sont opposés en leur sommet alors il sont égaux.
Donc: BAC=64°
j'additionnent ABC et EAC et sa me donne 128 
sa ne me fait ps un angles plat ou est mon erreur ?
mais comment a tu mesurer l'angle BCA et BAC?
D'après le codage sur ta figure, quelle est la nature du triangle ABC?
quelle théorème utiliser pour trouver les mesures des angles BCA et BAC sachant que le triangle ABC est isocèle?
a oui ...
Donc
On sait que :
- ABC est isocèle en A
- ABC=32°
Or: quelle est le théorème correspondant ?
Donc : ACB=32°
On sait que :
ABC=32°
ACB=32°
Or : la sommes des angles d'un triangle est égale a 180°
d'ou: 180-(32+32)=116°
Donc : l'angle BAC mesure 116°
Ensuite pour prouver que les points BAE sont alignés je sait qu'il faut que j'additionne les deux angles opposé BAC et EAC ce qui me donne 180°, qui représente un angle plat mais comment espliquer ce-ci en utilisant des théorème et comment en déduire qu'il sont aligner sachant qu'il sont sur un angle plat.
Bonjourn
c'est louable de se poser des questions fondamentales de base comme
pourquoi trois points alignés sont ils sur une même droite ?
ou des trucs du même genre sur la définition d'un angle plat.
mais faut pas pousser trop loin dans cette direction sous peine d'être bloqué par des définition même de ce qu'est réellement un angle, question qui est réellement insoluble "au niveau collège"
par définition "trois points P Q R sont alignés dans cet ordre" est équivallent à "angle PQR = 180°"
(ou QPR = 0° etc ...)
Bonjour,
je sais qu'il sont alignés ses 3 points ! mais je penser devoir donner une définition pour dire un angle plat est une ligne droite et je ne connaissait pas de définition exacte pour le prouver mais j'ai demander a mon professeur qui ma juste demander une déduction et non une définition donc maintenant je sais.
tu sais que l'angle fait 180° (par le calcul des angles), donc ils sont alignés (par définition de ce qu'est un angle plat :
"trois points P Q R sont alignés dans cet ordre" est équivallent à "angle PQR = 180°"
angle = 180
 points alignés.
points alignés.
la déduction demandée c'est juste ce petit mot "donc"
tu ne sais pas au départ s'il sont alignés ou pas
tu calcules les angles (directement comme tu l'as fait)
de ce calcul et rien que de ce calcul tu obtiens l'angle = 180°
donc les points sont alignés (et seulement maintenant tu le sais, seulement après avoir calculé l'angle) c'est cela une "déduction".
et une déduction se justifie par une propriété (définition / théorème)
je sais que l'angle est de 180° (parce que je l'ai calculé)
or par définition un angle plat est formé de points alignés
donc les points sont alignés.
D'accord voila ce que je ne comprenais pas enfaite ces tout simple merci a toussent de m'avoir aider pour cette exercice 
2) en revanche pour le petit 2 ont me demande juste la nature du triangle
une petite remarque sur la question 1)
les deux angles opposé BAC et EAC
de sorte que l'angle BAE = BAC + CAE
oui, pour le 2) c'est bien ce qu'on te demande.
(et la réponse n'a pas encore été abordée ici)
pour le justifier tu peux utiliser AB=AC=AE et la question 1 pour dire que C est sur le cercle de diamètre BE, cercle suggéré par la figure de Mijo.
d'accord pour la 2) je pourrai donc utiliser le théorème si un triangle est inscrit dans un cercle don un diamètre est un coté de ce triangle alors il est rectangle son hypotenuse est un diamètre du cercle.
parce que AB = AC = AE (c'est dans l'énoncé, et je te l'avais remarqué)
donc B, C, E sont sur un cercle de centre A et de ce rayon.
d'autre part tu viens de démonter que le centre A et B et E sont alignés, donc BE s'appelle un diamètre.
(et C est sur ce cercle donc ce cercle s'appelle le cercle circonscrit)
voila ce que j'ai fait pour le 2)
Dans ce triangle, on a AC=AB=AE donc la médiane AC mesure la moitié du coté BE et le cercle de diamètre BE de centre O passe par A. AC=1/2 de BE.
Or: si dans un triangle la longueur de la médiane issue d'un sommet est égale a la moitié de la longueur du coté opposé, alors ce triangle est rectangle en ce sommet.
Donc: BCE est rectangle en C.
c'est la même chose, et c'est presque bon.
le cercle de centre O (c'est quoi O ???) n'a rien à faire là dedans.
le cercle de diamètre BE ne risque de toute façon pas de passer par le milieu de son diamètre BE !!!! quoi qu'il arrive. c'est idiot.
le mieux, tu ne parles pas de ce cercle du tout qui n'a rien à faire avec la propriété que tu cites (médiane = moitié d'un côté)
tu dois tout de même noter pourquoi AC, AB et BE sont la moitié de BE : c'est parce que ABE sont alignés.
sinon il n'y aurait aucune raison avec simplmemnt AB=AE que ce soit égal à la moitié de BE
ma méthode avec le cercle de diamètre BE était une autre propriété que celle que tu utilises (triangle inscrit dans un demi-cercle)
mélanger les deux méthodes ne donne rien de bon.
d'accord merci alors j'oublie le cercle et je m'était tromper ce n'était pas de centre O mais A donc Dans ce triangle, on a AC=AB=AE car les points ABE sont alignés donc la médiane AC mesure la moitié du coté BE. AC=1/2 de BE.
Or: si dans un triangle la longueur de la médiane issue d'un sommet est égale a la moitié de la longueur du coté opposé, alors ce triangle est rectangle en ce sommet.
Donc: BCE est rectangle en C.
la rédaction correcte est de mettre les "car" et les "donc" au bon endroit !
c'est pas pour faire joli c'est pour dire quelles sont les hypothèses et quelles sont les conclusions
AC = AB = AE car ... c'est marqué dans l'énoncé.
pas parce que ABE alignés !!
ensuite
AB = AE et ABE alignés donc A est le milieu de BE et AC = AE = AB = 1/2 BE
donc la médiane AC mesure la moitié du côté BE.
la suite OK.