Inscription / Connexion Nouveau Sujet
TIPE : une démonstration géométrique.
Bonjour à tous !
J'étudie la théorie du chaos dans mon TIPE et plus particulièrement un exemple de système non chaotique.
Cet exemple, c'est le lancer d'une boule de billard sur un tapis de billard, avec différentes trajectoires initiales (voir l'image).
Il apparaît que quelle que soit la trajectoire initiale imposée, la boule revient toujours, même après un nombre de rebonds très grand, à son point de départ.
C'est sur ce point (c'est le cas de le dire) que je compte m'appuyer pour assurer que ce système n'est pas chaotique : il forme une boucle. Cependant je vois gros comme une maison la question du jury : " Vous avez dit que la boule revenait obligatoirement à son point de départ, vous pouvez nous le démontrer ? ".
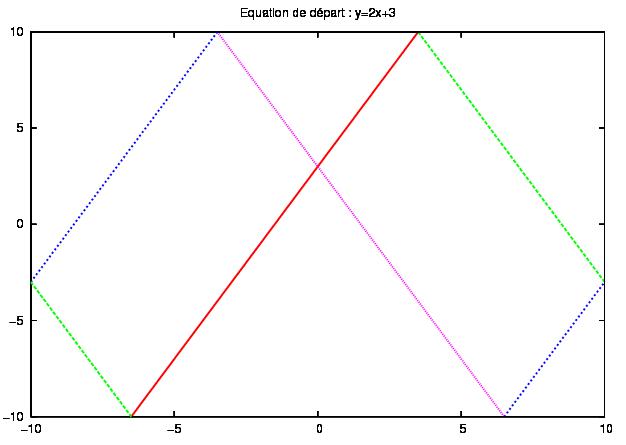
Alors voilà, je fais appel à vous... Je suppose que je dois me placer dans un repère orthonormé (O, i, j), que je dois, par une équation, délimiter ma surface d'étude et par une équation de la forme y=ax+b, démontrer que je retombe à un moment ou un autre sur mes pieds... Vous auriez une idée ? Ou bien est-ce que la démonstration dépasse mon niveau de MPSI ?
Je compte faire pareil avec un cercle, si je peux m'en sortir avec une surface carrée, ça sera déjà bien...
Bonjour,
Pb classique (pour ce qui est du rectangle)si mes souvenirs sont bons.
Tu imagines un pavage infini fait avec ton rectangle Tu pars d'une bande (cela revient au même modulo quelques aménagements), ton trajet avec les rebonds peut se représenter par symétrie comme une ligne droite qui traverse ton pavage. Travail sur cette piste pour que le trajet ne soit pas chaotique, il me semble qu'il y a un rapport entre les proportion de ton rectangle et la pente de ta droite (Rapport rationnel peut-être..?)
salut
en notant p et q les longueur et largeur du rectangle alors :
le coefficient directeur d vérifie donc nq = dnp où n est entier ....
ce me semble-t-il ....
carpediem, est-ce que tu es parti sur la piste de DOMOREA ?
Si j'ai bien compris, trouver un rapport entre les proportions du rectangle et la pente de ma droite (d'ailleurs quelle droite, n'importe laquelle ?) tendrait à montrer que je retombe d'où je suis parti ?
bien sur ....imagine le pavage du plan et considère uniquement la droite en pointillé bleu .... le petit morceau à droite ...(mais tu peux le faire avec n'importe laquelle...)
origine en bas à gauche ... équation y = d(x - a)
f(a + np) = f(a) + nq
....
On pose l'origine en bas à gauche.
L'équation y = d(x-a) correspond à la droite en pointillé bleu en bas à droite, n'est-ce pas ?
Avec d = coefficient directeur, mais à quoi correspond a ?
Quant à f, c'est la fonction qui est associée à la droite y=d(x-a) ?
Si oui, f(a+np) = f(a) + nq est obtenu de quelle façon ?
Merci
f(a) = 0 tout simplement ....
revenir "au même point A(a,0)" signifie que lorque tu te déplaces de n rectangles vers la droite (donc de np) tu montes de n rectangles (donc de nq) et le rapport est donc la pente de la droite ...
bonjour,
Je te laisse cogiter sur le rectangle, tu as eu suffisamment d'informations.
Pour le cercle, c'est très simple.
Fais une figure (cercle de centre O, tu pars d'un point A du cercle dans une direction AB B sur le cercle (et par exemple sens direct )telle que ). La perpendiculaire à la tangente au cercle en B passe par O, On a
En recommençant tu effectues une suite de rotations du même angle
Pour retomber sur ton point de départ il y a une condition nécessaire et suffisante sur la valeur de
La vois-tu ?


 géométrie en post-bac
géométrie en post-bac