Bonjour,

Vrai si M est le milieu de [AB].
rapport harmonique ?

bonsoir à tous

et oui j'ai encore besoin d'un renseignement pour encore une fois demontrer que les droites sont paralleles.

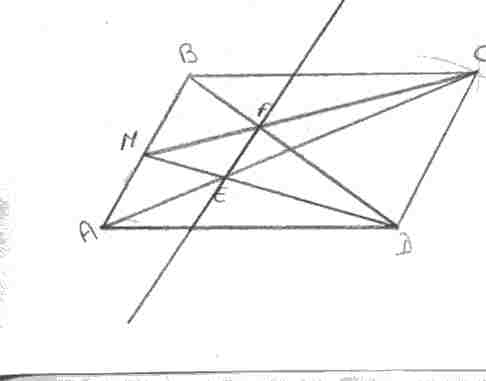
  Comment demontrer que [EF] est parallele à [CD] sur le shema ci-dessous en ayant comme renseignements:
(ennonce du devoir)
Les digonales d'un parallelogramme ABCD se coupe en I; M est le milieu du cote [AB].Les segments [MD]et [AC] se coupent en E. Les segments [MC] et [BD] se coupent en F.

Merci encore pour tes conseilles.




*** message déplacé ***

bonjour
je pense qu'il faut utiliser la réciproque de thalese
si tu reussit  a montrer que IC/IE= ID/IF alors tu pourra deduir que les droites  EF ET CD sont // ,de meme tu peux appliquer la réciproque dans le triangle ABI

si IF/IB=IE/IA alors on aura EF  // BD et comme BD est // a CD on aura CD // EF

a moins que dans les etudes supérieurs ya d'autre methodes pour demantrer ca

*** message déplacé ***

manuRS,

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

Bonsoir ManuRS !

Appelons O le centre du parallélogramme (ce qui n'est pas dit dans l'énoncé !!!).
La symétrie oblique (ou affine) d'axe OM (M = milieu de [AD], non dit !!!) et de direction AB applique successivement
A sur D
B sur C
C sur B
M sur M
donc
AC sur DB
BM sur CM
AC BM sur DB CM
E sur F.
Par conséquent, EF est parallèle à AD.

Si tu ne connais pas les symétries obliques, alors tu peux résoudre le problème
soit dans le cadre de la géométrie analytique,
soit dans celui de la géométrie vectorielle,
soit à l'aide d'homothéties,
soit dans le plan complexe.

Au plaisir.

Merci pierre et flashy.

merci pour vos reponse mais pierre peux tu me mettre sur la voie quand tu parles de geometrie vectorielle car je vais essayer d'explorer cette idée.

merci

Bonsoir ManuRS !

En gras, ce sont des vecteurs, sinon ce sont des réels.
Posons AB = p AC et BE = q BM.
On a AB = AE + EB = p AC - q BM = p (AB+BC)- q (BA + AD/2) = (p+q) AB + (p-q/2) AD.
D'où, p+q=1 et p-l/2=0.
Donc, p=1/3 et q=2/3.
Ainsi, BE = 2/3 BM.
De la même manière, on obtient CF = 2/3 CM.
Aussi, EF = EB + BC + CF = -2/3 BM + BC + 2/3 CM = BC + 2/3 CB = 1/3 BC.
Par conséquent, les droites EF et BC sont parallèles.

Est-ce assez clair ?

Au plaisir.

merci pierre mais la je crois que je nage la brasse coulé je n'ai pas vu tout ça en troisieme.
il n'u*y a pas vraiment plus simple car je ne vois pas comment je vais expliquer a mon professeur cette demonstration. Amoins de lui dire de telephoner a M. Pierre hihihihi .

merci comment meme pierre

merci pierre mais la je crois que je nage la brasse coulé je n'ai pas vu tout ça en troisieme.
il n'u*y a pas vraiment plus simple car je ne vois pas comment je vais expliquer a mon professeur cette demonstration. Amoins de lui dire de telephoner a M. Pierre hihihihi .

merci comment meme pierre