Inscription / Connexion Nouveau Sujet
Tracer une fonction f(x,y) =0
Bonsoir,
On me demande de tracer l'équation :
3y^2 - 3x^2 +16y -4x + 20= 0
Je ne vois ps si y a une théorie la dessus et ce qu il faut faire.
Merci d avance !
bonjour
tracer l'équation ?
ce ne serait pas plutôt l'ensemble dont ceci est une équation ?
mets sous forme canonique, et reconnais une hyperbole équilatère.
Bonjour lafol,
l equation est en faite
donc la forme canonique me donne :
comment tu détermines les asymptotes les minimums....
Je ne vois vraiment pas comment faire merci !
3)2
ca me donne
mais je vois tjs pas comment je peux tracer la courbe qu on me demande ... ni quelle tete elle peut avoir !
Bonsoir.
Je confirme : l'ensemble étudié s'écrit bien
(x + y - 2).(3x - 3y + 10) = 0
En appliquant la règle du produit nul : x + y - 2 = 0 ou 3x - 3y + 10 = 0
L'ensemble est donc la réunion de deux droites : y = - x + 2 et y = x +
C'est le genre hyperbole équilatère dégénéré en ses deux asymptotes.
je n'avais pas fait la mise sous forme canonique (et pas pensé à l'éventualité d'une hyperbole dégénérée, je le confesse 
)
Merci raymond,
mais je pensais que c'était moins brutal que l'intersection de 2 droites que ca ressemblais plus a des paraboles avec une sorte d arrondie !
Sinon à quel endroit se situe les points tels que
Bis : Si on avais
ca m'aurait donne quoi ?
Pour l'inéquation.
(évite de garder le "-" devant en passant à > 0)
Tu sais qu'une droite (D) d'équation ax + by + c = 0 partage le plan en deux régions, dont la frontière est (D).
Dans l'une des deux régions ax + by + c > 0, et dans l'autre ax + by + c < 0
Pour connaître la région + et la région - on prend un exemple.
Tu dois donc construire tes deux droites, chercher les régions + et -, puis regarder celle(s) qui correspondent à ton inégalité.
Pour l'équation.
On peut réduire en :
Tu as le type hyperbole équilatère.
Ok nickel je commence à saisir !!
par contre avec l equation je vois pas comment on retrouve les 2 droites :/
et comment je peux la trouver???
car avant j ai bien compris que c 'était un cas particulier!
Dans ce cas que dois je étudier pour pouvoir la tracer???
Merci d avance !
déjà, (y-8/3)² = a/3 + (x+2/3)² : en supposant a positif, il n'y a aucun point dans la bande "y" compris entre 8/3 - racine(a/3) et 8/3 + racine(a/3).
le centre de l'hyperbole est de coordonnées (-2/3 ; 8/3)
je fais de l'archéologie (mes vieux bouquins de quand j'étais en term' 
) et je complète demain (sauf si Raymond repasse par là avant moi)
Bonsoir lafol.
Je t'imagine comme Gaston en train de se faire une cabane dans les archives de la rédaction !!
Je vais essayer de t'éviter cela.
suistrop : tu n'as pas compris.
Si l'on a :
alors, c'est la forme A² - B² = 0. Tu as vu dès la troisième que :
A² - B² = 0 
(A + B)(A - B) = 0 A + B = 0 ou A - B = 0 (théorème du produit nul).
Par contre, avec a 
0, et
plus question de se ramener à un produit nul
Alors, on peut procéder comme te le signale lafol.
On peut aussi :
1°) prendre une nouvelle origine 
en posant :
Avec :
L'équation s'écrit alors :
2°) Maintenant, il faut distinguer les cas a > 0 ou a < 0
¤ Si a > 0, je pose a = b². On écrit :
Ce résultat s'appelle l'équation réduite de l'hyperbole (équilatère ici).
¤ Si a < 0, je pose a = - b². En changeant tous les signes, on se ramène à :
Pour en revenir a ca,j avais pas tout saisie je suis aller voir un prof de ma fac qui a pris le temps de m expliquer 
En effet c est pas sorcier et c est bien ce qu' a fais raymond !!! meme si je comprend pas pourquoi faire 2 cas en fct de a postif ou négatif !
X=(ax+b)
Y=(cx+d)
X² - Y²= a
(X+Y)(X-Y)=a
la on change de repere en se placant dans X+Y = X' et X-Y = Y'
X'Y'=a
donc
Y'=a/X'
Hyperbole dans le nouveau repere
Merci d'avance de me corriger
Annuler
connectez vous
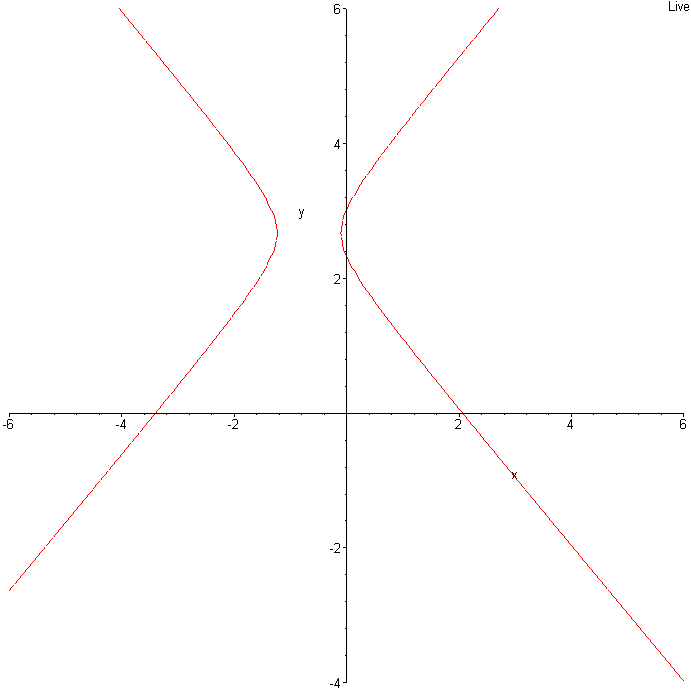
géométrie en post-bac