Bonjour seb9563,

Tu sembles nouveau sur le forum. Sois le bienvenu.
Il me semble important de commencer par en respecter les règles.
Tu as le droit de poster un scan de la figure, mais de la figure seulement.
En revanche, il faut recopier la partie "texte" de l'énoncé, pour (i) qu'elle soit accessible par le moteur de recherche, (ii) faire un petit effort.
Fais-le, puis nous t'aiderons.

Nicolas

PS - L'image d'une droite par une homothétie est une droite parallèle. Cette propriété du cours permet de résoudre facilement a) et b), non ?

ok, en effet je suis nouveau, voici le bon post:

Sur la figure ci-dessous, AB CD est un rectangle de sens direct, AEFB et ADGH sont des carrés de sens direct.



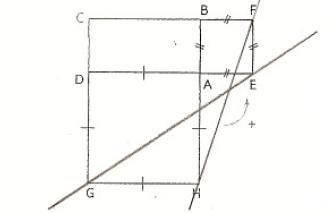
Le but de l'exercice est de démontrer que les droites (AC), (EG) et (FH) sont concourantes.
Pour cela, on note I le point d'intersection des droites (EG) et (FH) et on introduit:
. l'homothétie hl de centre 1 telle que hl (G) = E;
. l'homothétie h2 de centre 1 telle que h2(F) = H.

al Quelle est l'image de la droite (CG) par h1 puis par la composée h2 0(rond) hl ?

b) Quelle est l'image de la droite (CF) par la composée hl 0(rond) h2 ?

c) Justifiez l'égalité h2 0 hl = hl 0 h2. Déduisez-en que la droite (AC) passe aussi par le point I.

édit Océane : image placée sur le serveur de l', merci d'en faire autant la prochaine fois

Je répète : "L'image d'une droite par une homothétie est une droite parallèle. Cette propriété du cours permet de résoudre facilement a) et b), non ?"

Que proposes-tu ?

a ) ce serait la droite FE l'image de Cg par H1? et par la composé c'est BH?

b)ce serait DE?

mais j'ai du mal a le prouver...parceuqu'on connait pas lesmesures exactes

Je ne vois pas pourquoi tu as besoin des mesures.

Je ne comprends pas tes notations non plus.
- les droites se notent entre parenthèses
- qui est Cg : est-ce (CG) ?
- qui est H1 ? est-ce h1 ?

a)
L'image de (CG) par h1 est la parallèle à (CG) passant par h1(G)=E : il s'agit donc de (FE)
L'image de (FE) par h2 est la parallèle à (FE) passant par h2(F)=H : il s'agit donc de (AB).

En résumé :
h1((CG)) = (FE)
h2oh1((CH)) = (AB)

b)
De même, h1oh2((CF)) = (AD)

c)
Or h1oh2 = h2oh1 (à justifier)
Donc h2oh1((CF)) = (AD)

h2oh1 est une homothétie de centre I.
C est l'intersection de (CH) et (CF)
donc h2oh1(C) est l'intersection de h2oh1((CH)) et h2oh1((CF)), c'est-à-dire l'intersection de (AB) et (AD), c'est-à-dire A.
h2oh1 est donc une homothétie de centre I envoyant C en A.
Donc I, A, C alignés
Donc (AC) passe par I.

Sauf erreur.