Bonsoir,
Dans le cas où les 4 triangles sont d'aire égale, alors chacun des triangles devrait valoir le quart de l'aire du trapèze.

Si vous assemblez les deux triangles qui sont adjacents à l'angle droit du trapèze, vous obtenez un triangle dont l'aire devrait valoir la moitié de celle du trapèze.

La formule de l'aire de ce nouveau triangle devrait vous permettre de conclure.

Bonjour brojer, voici mon exercice en photo. En fait, quelqu'un dit que A1 est plus grande que A2, il faut vérifier si il a raison ou si il a tort. Je rappelle que j'ai aucune dimension.

Je ne vois pas la photo, mais en supposant que A1 est la petite base, A2 la grande base et h la hauteur.
L'aire du trapèze serait .
L'aire du triangle rectangle compris formé par la grande base, la hauteur et une des diagonales est .
Si les triangles sont égaux alors, l'aire du triangle devrait valoir la moitié de l'aire du trapèze. Or dans l'aire du trapèze intervient le paramètre A₂, qui n'intervient pas dans l'aire du triangle, donc on constate que les triangles ne sont pas forcément égaux

Bonjour brojer, voici la photo.
En fait quelqu'un affirme que A1 et plus grande que A2.
PS: il ne me semble pas que DIC soit rectangle... à moins qu'il le soit obligatoirement avec les diagonales du trapèze... Je suis perdu...

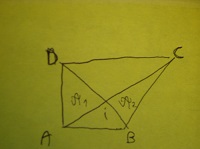
J'étais arrivé à la conclusion que les aires des triangle BAD et BDC n'étaient pas forcément égales en disant que BAD est rectangle en A.
Je réfléchis à un moyen de montrer que les aires des triangles ADI et BIC sont différentes.

Ok stp aide moi, je suis vraiment perdu...

Alors les aires A1 et A2 sont effectivement égales. Je cherche encore le moyen de le montrer simplement

Ok, les triangles BAD et BAC ont la même aire, car ils ont la même base AB et la même hauteur (la hauteur du trapèze).

Si on enlève l'aire du triangle ABI au triangle BAD, on obtient l'aire du triangle AID.
Si on enlève l'aire du triangle ABI au triangle BAC, on obtient l'aire du triangle BIC.

Donc c'est reglé-

Autrement dit :