Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau autre
Partager :

triangle équilatéral

Posté par l1pc (invité) 21-10-06 à 15:17

bonjour,
nous n'arrivons pas à faire une question d'un devoir maison qui nous empèche de faire la suite, si vous pourriez nous aider ce serait gentil!
"Si ABCDEF est un hexagone inscrit dans un cercle C(0,R), de sorte que AB=CD=EF=R, alors les milieux respectifs P,Q,R des segments [BC],[DE],[FA], sont les sommets d'un triangle équilatéral. "

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 15:19

Bonjour,

R est à la fois un point et une distance ?
Est-ce aussi le rayon du cercle ou pas ?

Posté par l1pc (invité)re : triangle équilatéral 21-10-06 à 15:20

R est le rayon du cercle de centre O
merci d'essayer de nous aider

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 15:27

Vous connaissez la notion de nombre complexe, d'argument, etc... ?

Posté par Dasson (invité)re : triangle équilatéral 21-10-06 à 15:49

O est équidistant de P, Q, R (apothème de l'hexagone) donc centre du cercle circonscrit à PQR.
POR=ROQ=QOP=120°.

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 15:50

Voici déjà une figure.
(merci TeXgraph)

triangle équilatéral

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 15:51

Bonjour Dasson
Es-tu sûr de toi ?

Posté par l1pc (invité)re : triangle équilatéral 21-10-06 à 15:54

oui on connait les notions que tu as énoncé

Posté par Dasson (invité)re : triangle équilatéral 21-10-06 à 15:56

Bonjour Nicolas.
J'ai lu hexagone régulier, un mirage sans doute

Posté par
Tigweg Correcteurre : triangle équilatéral 21-10-06 à 16:05

Bonjour à vous tous

Oui, j'ai l'impression que le plus efficace est de passer par les complexes, je ne vois aucun argument géométrique simple...

Dasson> Pourrais-tu définir ce qu'est l'apothème d'un hexagone s'il-te-plaît?
Je n'ai jamais entendu ce mot!
Merci!

Tigweg

Posté par Dasson (invité)re : triangle équilatéral 21-10-06 à 16:23

Apothème : distance du centre à un côté d'un polygone régulier...
Souvenir de jeunesse

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 16:29

Je viens de finir au brouillon une démonstration avec les complexes. Mais c'est bourrin.

Posté par
Tigweg Correcteurre : triangle équilatéral 21-10-06 à 16:31

Ok merci Dasson
C'est vrai qu'à une époque le programme de géométrie était autrement plus fourni qu'à l'heure actuelle
(A "mon" époque, càd il y a 15 ans, il avait déjà sacrément diminué )

Tigweg

Posté par
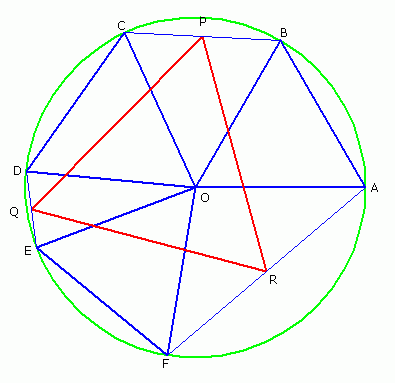
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 17:07

On peut supposer, sans perte de généralité que :
- le centre du cercle est l'origine
- le rayon du cercle est 1
- par conséquent, le cercle est le cercle trigonométrique
- A,B,C,D,E,F se suivant dans le sens direct
- l'affixe de A est 1

On note les angles \alpha et \beta comme sur la figure.

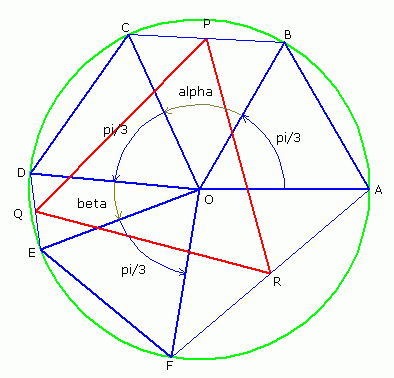
triangle équilatéral

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 17:07

On note \fbox{\varepsilon=e^{i\frac{\pi}{3}}}
De \varepsilon^3=-1, on tire :

\fbox{\frac{1}{\varepsilon}=-\varepsilon^2}
De 1+e^{i\frac{2\pi}{3}}+e^{i\frac{4\pi}{3}}=0, on tire

\fbox{\varepsilon-1=\varepsilon^2}

On a alors les affixes suivantes :
A : 1
B : e^{i\frac{\pi}{3}}=\varepsilon
P : \frac{\varepsilon\left(1+e^{i\alpha}\right)}{2}
C : e^{i\left(\frac{\pi}{3}+\alpha\right)}=\varepsilon .e^{i\alpha}
D : e^{i\left(\frac{2\pi}{3}+\alpha\right)}=\varepsilon^2.e^{i\alpha}
Q : \frac{\varepsilon^2.e^{i\alpha}\left(1+e^{i\beta}\right)}{2}
E :

e^{i\left(\frac{2\pi}{3}+\alpha+\beta\right)}=\varepsilon^2.e^{i(\alpha+\beta)}
F : e^{i\left(\pi+\alpha+\beta\right)}=-e^{i(\alpha+\beta)}
R : \frac{1-e^{i(\alpha+\beta)}}{2}

Donc z_P-z_R \\ \\ =...=\frac{\varepsilon^2+\varepsilon.e^{i\alpha}+e^{i(\alpha+\beta)}}{2}

Et z_Q-z_R \\ \\ =...=\varepsilon\,\frac{\varepsilon^2+\varepsilon.e^{i\alpha}+e^{i(\alpha+\beta)}}{2}=\varep \\ \\ silon\left(z_P-z_R\right)

Donc Q est l'image de P par la rotation de centre R et d'angle pi/3
Donc le triangle PQR est équilatéral.

Sauf erreur.

Nicolas

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 17:09

Ce message se substitue au précédent.

On note \fbox{\varepsilon=e^{i\frac{\pi}{3}}}
De \varepsilon^3=-1, on tire : \fbox{\frac{1}{\varepsilon}=-\varepsilon^2}
De 1+e^{i\frac{2\pi}{3}}+e^{i\frac{4\pi}{3}}=0, on tire \fbox{\varepsilon-1=\varepsilon^2}

On a alors les affixes suivantes :
A : 1
B : e^{i\frac{\pi}{3}}=\varepsilon
P : \frac{\varepsilon\left(1+e^{i\alpha}\right)}{2}
C : e^{i\left(\frac{\pi}{3}+\alpha\right)}=\varepsilon .e^{i\alpha}
D : e^{i\left(\frac{2\pi}{3}+\alpha\right)}=\varepsilon^2.e^{i\alpha}
Q : \frac{\varepsilon^2.e^{i\alpha}\left(1+e^{i\beta}\right)}{2}
E : e^{i\left(\frac{2\pi}{3}+\alpha+\beta\right)}=\varepsilon^2.e^{i(\alpha+\beta)}
F : e^{i\left(\pi+\alpha+\beta\right)}=-e^{i(\alpha+\beta)}
R : \frac{1-e^{i(\alpha+\beta)}}{2}

Donc z_P-z_R =...=\frac{\varepsilon^2+\varepsilon.e^{i\alpha}+e^{i(\alpha+\beta)}}{2}

Et z_Q-z_R =...=\varepsilon\,\frac{\varepsilon^2+\varepsilon.e^{i\alpha}+e^{i(\alpha+\beta)}}{2}=\varepsilon\left(z_P-z_R\right)

Donc Q est l'image de P par la rotation de centre R et d'angle pi/3
Donc le triangle PQR est équilatéral.

Sauf erreur.

Nicolas

Posté par l1pc (invité)re : triangle équilatéral 21-10-06 à 18:09

merci bcp pr ton aide

Posté par
Nicolas_75 Correcteurre : triangle équilatéral 21-10-06 à 18:11

Je t'en prie.


Rechercher
Menu
Espace membre
23 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1715 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !