Inscription / Connexion Nouveau Sujet
Triangle isocèle
Bonjour à tous je viens de devenir membre de ce site car je pense que vouz allez pouvoir m'aider...
J'ai un DM de Maths et je ne comprend pas bien ce que je doit faire je suis bloqué sur mes reponses sans savoir quoi utiliser.
Voici:
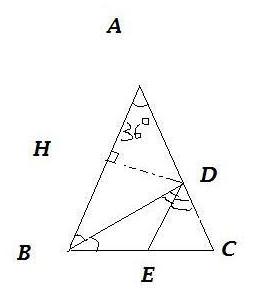
ABC est un triangle isocéle en A, BAC=36° et BC=4 CM. La bissectrice de L'angle ABC coupe [AC] en D et celle de l'angle BDC coupe [BC] en E.
Démontrez que les triangles ADB et DBC sont isocèles ainsi que les triangles EDC et BDE
Je suis bloqué car je pense que pour demontrer que le triangle ADB est isocèle je peux utiliser l'axe de symetrie H que coupe AB mais d'autre je crois pouvoir calculer aussi mais je ne sais pas comment je sais pas comment commencer l'exercice je voulais des conseils pour cela.
Merci beaucoup!
Voici l'image:
Il faut calculer...
Que vaut la somme des mesures des angles d'un triangle ?
Quelle est la propriété des deux angles à la base d'un triangle isocèle ?

La somme des mesures des angles d'un triangle vaut 180°...
Et un triangle est isocèle si 2 angles sont egaux mais la je connais que la mesure d'un angles alors je peux pas dire que 2 sont egaux car je connais qu'un...
Je dois utiliser la trigo??
Mais comment calculer si je connais que la mesure de l'angle ABC??
La mesure de l'angle en A vaut 36°
La somme des trois mesures vaut 180°
Que vaut la somme des mesures des angles en B et en C ?
Quelle est donc la mesure de ces angles en B et en C ?

Mais bien sûr !
Et quand tu divises en deux l'angle en B par la bissectrice... combien vaudra chaque moitié de cet angle en B ?

Eh oui... tiens, comme la valeur de l'angle en A !
Ce n'est pas un hasard. Et cela doit t'être utile pour la résolution de ton exercice !

Oui cela m'est beaucoup utile Mercii!!
Donc je sais que la somme d'un triangle vaut 180°
La somme des angles B et C vaut 144 et et les mesures de ces angles vaut 72°
Le angle B coupe pas la bissectrice vaut 36° alors le triangle ADB est isocèle en D.
Mais pour le triangle BDC je sais que l'angle B vaut 36° et que l'angle C vaut 72°
Donc pour savoir combien vaut l'angle D je dois utiliser la trigo? mais comment utiliser la trigo ici?
Il n'y a pas à utiliser la trigonométrie.
Dans le triangle BDC, tu connais les mesures des angles en B ( = 36° ) et en C ( = 72° )
Que vaut donc la mesure de l'angle en D ?
Et que vaut la mesure de la moitié de cet angle quand il est divisé en deux par une bissectrice ?

Je vois maintenant ça commence a renter!
Donc 180°-(36°+72°)
= 72°
/2= 36°
Le triangle BDC est donc isocèle en C
merci beaucoup!!!
J'ai encore quelques problemes avec ce triangle mais la je suis completement bloqué sur la suite, j'espere que tu puisse m'aider de nouveau...
Bon la question c'est:
On pose AB=AC=X
Demontrer que DC=x-4 et que EC= 8-x
Puis a l'aide tu Theoreme de Thales appliqué à des triangles convenablement choisis , demontrez que:
8-x = x-4
4 x
J'arrive pas a comprendre comment demontrer ça je suis completement bloqué.
Merci
Tu connais BC = 4
Tu connais AB = AC = x
Tu as démontré de nombreux triangles isocèles.
Il est facile de calculer
DC = x - 4
EC = 8 - x
Ensuite, ces nombreux triangles isocèles et les égalités d'angles que tu as trouvées te permettent de démontrer qu'il y a des droites parallèles dans cette figure. Puis... théorème de Thalès (programme du collège ! ).

Merci pour m'avoir repondue!
J'ai beacoup de soucis avec la geometrie, j'aime les calcules mais pas geometriques...
Bon mais j'ai une idée pour calculer DC
Je sais que le triangle ABC est isocèle en A et que AB=AC=X
Et je sais que BC= 4
je sais aussi que les droites (DE) et (AB) Sont parallèles
Donc je peux dire que
AC-BC= DC
x - 4 = DC ???
C'est la seule solution que j'ai trouvé.
Mais après pour EC = 8-x j'aucune idée je ne voit pas de tout d'où il peut venir ce 8.
Pour le moment le fait que les droites (DE) et (AB) soient parallèles n'est pas utile (pas encore, ça va venir...)
Tu as montré que le triangle ADC est isocèle en D c'est-à-dire que AD = BD
tu as aussi montré que le triangle BDC est isocèle en B c'est-à-dire que BD = BC
Donc... AD = BD = BC = 4
Or DC = AC - AD
donc DC = x - 4
Il faut que sur ta figure tu marques clairement toutes les égalités de longueurs (triangles isocèles) que tu connais (les égalités d'angle, cela serait aussi une bonne idée qui va servir ensuite).
EC = BC - BE
tu connais BC = 4
Tu as tout ce qu'il faut pour trouver la longueur BE

Merci beaucoup même mon prof de maths n'arrive pas a expliquer les choses clairement...
Vous n'imaginez même pas comment vous m'avait aidé!
Mercii
Pour EC = BE - BC
Donc EC = x-4 - 4
EC = x-8
et Voila...
j'ai presque reussi...Merci
il y a une derniere question que j'ai pas reussi c'es la suivante:
Déduisez-en que (x-2)²= 20 et que x = 2+2  5
5
J'essaie de developper le premier mais ça me donne pas 20 comme resultat.
Et pour le 2eme x doit être AC dont j'ai connais DC que vaut x-4 Et AD que vaut 4...
Je ne comprends pas.
Il faudrait que tu recopies correctement (exactement...) l'énoncé depuis quelques questions précédentes ; sinon on ne peut pas savoir à quoi se refère "déduisez-en..."

La questions precedente c'etait:
A l'aide tu Théorème de Thalès appliqué à des triangles convenablement choisis, demontrez que:
8-x = x-4
4 x
Après c'est la question dont j'ai parlé.
Ah oui...
"Produit en croix" pour cette égalité :
et tu dois trouver (après quelques calculs) : (x - 2)2 - 20 = 0

ça marche pas vraiment avec moi
J'ai trouvé ça:
Par produit en croix
8-x = x-4
4 x
8x-x² = 4x-16
8x-4x-x² = 16
4x-x² = 16
(x-2)² = 16
Je suis nul


