Inscription / Connexion Nouveau Sujet
Triangle rectangle
Bonjour
On considère la figure ci-dessous à compléter sur le polycopié.
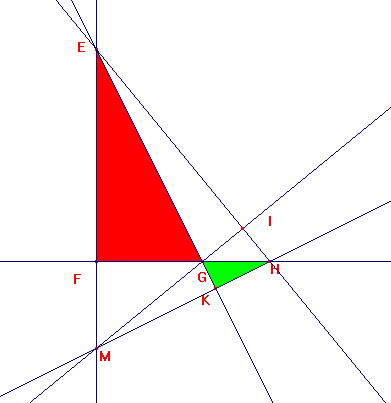
Le triangle EFG est rectangle en F et le triangle GHK est rectangle en K. On appelle M le point d'intersection des droites (EF) et (HK).
Démontrer que la droire (GM) est perpendiculaire à la droite (EH)
Dans le triangle EMH le point M est le sommet.
On sait qu'une hauteur d'un triangle est une droite qui passe par un sommet et qui coupe perpendiculairement le côté opposé.
donc La droite (GM) est perpendiculaire à la droite (EH).
Je ne peux pas joindre la figure. J'espère donc que c'est assez clair pour vous.
Je ne crois pas que ce soit cela. Pouvez-vous m'aider SVP, merci.
Stella
Non c'est toujours trop lourd ce que j'envoie
Il y a un triangle EFG rectangle en F. on prend le même point G pour faire l'autre triangle GHK rectangle en K. Les deux triangles se touchent au point G ce qui fait une seule figure. Les points EGK sont alignés et les points FGH sont alignés. Est-ce plus clair ?
Bonjour,
Dans le triangle EMH,
[E] et [HF] sont deux hauteurs qui se coupent en G, orthocentre.
[MI] est la troisième hauteur qui passe par G.
Les 3 hauteurs d'un tr sont concourantes en un poit ,orthocentre du tr.
Bonjour Stella,
Si tu considères le triangle EHM,
HF est la hauteur relative à H et coupe EM à angle droit
EK est la hauteur relative à E et coupe HM à angle droit
ces 2 hauteurs se coupent en G
la troisième hauteur passera par G et coupera EH à angle droit
A vérifier...
Philoux
oups...;
Caylus est passé par là, avec un dessin !
Avé Caylus !
Philus 
Oui Stella 
Et la géométrie, c'est pas mon fort... cf. ![]() Géométrie : 3 triangles dans un cercle...
Géométrie : 3 triangles dans un cercle...
Philoux


