Bonjour,
tu devrais joindre la figure....

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

je n'arrive pas a mettre un photo

Bonjour à vous deux
Peux-tu faire une figure avec Geogebra (logiciel gratuit chargeable sur Internet) et la transmettre.
Sinon décrire la figure le plus exactement possible
les droites AF et CF sont sécantes en F ?
les points A, B, E, F sont alignés dans cet ordre  (4 points)? et C, D, F aussi  (3 points)?
et connaît-on des longueurs de certains segments?
c'est probablement une application du théorème de Thalès

je suis entrain de télécharger le logiciel

voila la figure :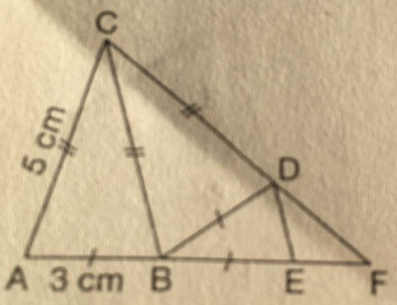



malou > ***tu t'es bien débrouillé(e) ! j'ai remis ton image dans le bon sens , la prochaine fois ce sera parfait ! ****

help s'il vous plaît 🤗

Bonjour,

Les triangles CBD et BDE sont-ils semblables ? Pourquoi ?

bonjour
justement c'est la question que je me posé les triangles CBD et ABC sont semblables car leurs mesures sont 2 à deux proportionnelles mais pour ce qui est de CBD et BDE je n'en sais rien je ne sais pas comment m'y prendre ...

Dans le triangle CBD, l'angle C a pour mesure (180- 2 fois l'angle CBD)  puisque = -triangle isocèle-

Dans le triangle BDE, l'angle DBE est égal à 180-angle ABC - angle CBD.
Or angle ABC = angle CBD (les triangles isocèles ABC et BDC sont égaux).

Donc l'angle C dans le triangle CBD =angle B dans le triangle BDE.
Ainsi les deux triangles sont semblables (un angle égal entre deux côtés égaux).

comment dois-je m'y prendre pour calculer les longueurs DE et DF ?

Bonjour
Les triangles CBD et ABC sont isocèles et plus que semblables, ils sont égaux
l'angle CAH est calculable  son cos est AH/AC
voir dessin fait avec Geogebra
On peut calculer l'angle DBE=180°-145,08°, puis l'angle DEB et on voit que BDE semblable à ABC car il est isocèle aussi et DE est dans le rapport de similitude BD/BC=3/5
d'où DE=3*3/5=9/5=1,8 cm
pour FD utiliser Thalès dans le triangle BCF car DE // BC (angles égaux par rapport à AE)
DE/BC=1,8/5=DF/5*DF
à finir

d'accord merci beaucoup je comprend mieux