Inscription / Connexion Nouveau Sujet
Triangulation
Bonjour tout le monde,
J'aurais besoin d'un petit coup de pouce. Voici l'énoncé :
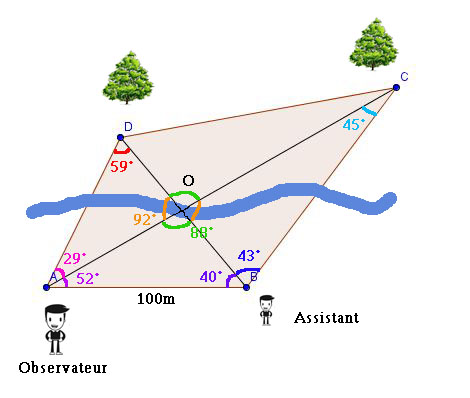
Un observateur placé en A cherche à mesurer la distance entre deux arbres dont les emplacements sont marqués par les points C et D. Ces arbres sont situés de l'autre côté d'une rivière infranchissable. Son assistant se place au point B.AB=100m.
L'observateur mesure les angles BAC et DAC : il trouve respectivement 52° et 29°.
Son assistant mesure les angles ABD et BDC : il trouve respectivement 40° et 43°.
Grâce à ces données, déterminer la distance entre les deux arbres.
Pour info : les topographes utilisent, pour mesurer les angles, un appareil appelé théodolite.
Dans cet exercice, j'a trouvé tous les angles à l'exception de deux : ODC et OCD
Je poste la figure que j'ai faite!
Mercie d'avance pour votre aide
(DM à rendre pour le 14 Février, journée des Amoureux)
Nulle-en-maths
Bonjour,
Ta figure n'a pas été postée.
Par ailleurs, pour l'assistant, le second angle BDC m'étonne un peu ; j'aurais plutôt vu DBC.
Tu fais ensuite intervenir un point O bien mystérieux.
Exact, c'est bien l'angle DBC, je me suis trompée en recopiant!
Le point O est le point d'intersection des diagoles de ABCD.
Sur la figure donnée par mon professeur aucun angles étaient présents sur la figure, appart ceux qui sont dans l'énoncé. J'ai trouvé les autres en faisant :
La somme des angles d'un triangles est égale à 180°
Donc:
AOB = 180 - BAC - DAC
AOB = 180 - 52 - 40
AOB = 88°
Ainsi de suite pour les autres.
Mais il me faut les logueurs et je crois qu'il faut que j'utilise la formule des sinus, sauf que je sais pas m'en servir! :$
Voila ce que donne la formule des sinus dans le triangle OAB :
OA/sin40 = OB/sin52 = 100/sin88.
Tu peux en déduire OA et OB.
Je trouve pour OB = 78.85 m et pour OA = 64.32m . Est ce que OB=OD ? Je pense que non, mais si ce n'est pas le cas, je ne vois pas du tout comment faire :/
Bonjour,
 Bravo pour OB et OA .
Bravo pour OB et OA .
Pour trouver OD , travaille dans le triangle AOD dans lequel tu connais OA et les angles.

 Merci de votre aide
Merci de votre aide 

