tout nombre entier naturel s'ecrit sous forme de (2^n) + k ;
avec k appartient à {0;1;2;.......;(2^n) -1} .avec  n appartient à IN*.

on va montrer par reccurence que tout nombre naturel verifie la conjecture de SYRACUSE . (C.S)

poor n = 1 ;on a (2^n) + k = 2 + k ;avec k appartient à {0;1} ; alors : (2^n) + k appartient à {2;3}.
on peut verifie facilement que 2 et 3 verifient la (C.S).

on suppose que la (C.S) est verifie pour n.

on va montrer qu'il'est verifie pour n+1.

on a (2^n+1) + k' ;avec k appartient à {0;1;2;.......;(2^n+1)-1}.

si (2^n+1) + k'  est pair c-à-d  k' appartient à {0;2;4;.......;(2^n+1)-2}.
avec k'=2S avec S appartient à {0;1;2;.......;(2^n) -1}.
alors (2^n+1) + k'  =  2((2^n) + S) avec S appartient à {0;1;2;.......;(2^n) -1}.
(2^n+1) + k'  =  2((2^n) + S)  est pair alors selon la conjecture on le divise par 2 ,on aura
(2^n) + S avec S appartient à {0;1;2;.......;(2^n) -1}.
selon l'hypothese de reccurence (2^n) + S avec S appartient à {0;1;2;.......;(2^n) -1} verifie la (C.S)
d'ou (2^n+1) + k'  ; avec k' appartient à {0;2;4;.......;(2^n+1)-2} verifie la (C.S).

selon la notion de reccurence tout nombre pair verifie la (C.S).

maintenant si (2^n+1) + k'  est impair c-à-d  k' appartient à {1;3;5;.......;(2^n+1)-1}.
(2^n+1) + k'  est impair selon la conjecture on le multiplie par 3 puis on l'ajoute 1.
certainemant on aura un nombre pair,et puisque tout nombre pair verifie la (C.S).
alors (2^n+1) + k' avec   k' appartient à {1;3;5;.......;(2^n+1)-1} verifie la (C.S).
d'ou tout nombre impair verifie la (C.S).

finalement tout entier naturel verifie la conjecture de SYRACUSE .

CONJECTURE DE SYRACUSE

Soit N un entier naturel.
Si N est pair, on le divise par 2.
Si N est impair, on le multiplie par 3 puis on l'ajoute 1.
En suivant cette algorithme (H) pour tout N de IN, on aura à la fin.
Mais pourquoi ?
Dans cet essai on va donner une démonstration pour affirmer la conjecture de SYRACUSE.
On dit que x vérifie la conjecture de SYRACUSE si en suivant l'algorithme (H) On aura à la fin 1.
On a IN : l'ensemble des entiers naturelles.
On définie les suites suivantes.
Soient f: IN ------¤   IN  ET:   g: IN ----¤   IN
         n   --------¤ n/2      n   -------¤ 3 n + 1

Soit: U: IN ---------¤   IN
.        n   --------¤   f (n) * g (n)
(*) : Signifie ou bien f (n) ou bien g (n).
Son tableau de vérié est :
f (n)        g (n)    f (n) * g (n)         V            V             F               V            F            V
F            V            V
F            F            F



       (n) vérifie la conjecture de SYRACUSE est équivaut à : il existe t appartient à IN tel que U0U0....0U=1.        (On a composé t (U)).
Soit K un élément de IN.
On va montrer par récurrence sur K que M = 8k+4 vérifie la conjecture de SYRACUSE.
Pour K=0, on a :M=4 et fof (M)=1.
Pour K : On suppose que M =8K+4 vérifie la conjecture, c à d, il existe m de IN tel que :
U0U­.. U0U (M) = 1.                                         (m compositions de (U))
On a: f0g0f0f (8K+4) = 3K+2
Alors : (U0..0U)0(f0g0f0f) (8K+4) = 1               (m-4 compositions de (U))
On pose : V = U0...0U                                      (m-4 compositions de (U))
D'ou il existe une suite V tel que : V (3k+2) = 1. Pour tout K de IN.
Pour k+1 : on a : M'  = 8(K+1) +4 = 8K+12.
On a (f0g0f0f)(8K+12) = 3K+5 = 3(K+1) +2
On pose K+1 = K'; alors (f0g0f0f) (M') = 3K' +2 avec : K' appartient à IN.
D'ou V0(f0g0f0f) (M') =  1.
Donc il existe m' de IN tel que :
U0U0­.. 0U0U (M') = 1.                              (m' compositions de (U))
D'ou M' vérifie lui aussi cette conjecture.
Selon le principe de récurrence la classe M= 8K+4 vérifie la conjecture de SYRACUSE.
      Alors : il existe t appartient à IN tel que U0...0U (M)=1.   (On a composé t (U)).
On a f0f (8K+4) = 2K+1    et   U0...0U0f0f (M)=1. (On a composé t-2 (U)).
On pose W = U0...0U             (On a composé  t-2 (U)).
D'ou W (2K+1) = 1 pour tout K de IN.
Alors il existe s = t-2 de IN tel que :
U0...0U(2K+1) =1.    Pour tout K de IN    (On a composé s (U)).
Alors tous les nombres impairs de IN vérifient la conjecture de SYRACUSE.
Si on a un nombre pair M'=2K (K de IN) alors : on divise M¡¯ par 2 jusqu'on obtient un nombre impair.  
Alors il existe m' de IN tel que : f0f.....0f M' = 2p +1, (On a compos¨¦ m'(f)).    (P de IN)
Donc (U0...0U)0(f0f0...0f) M' = U0...0U (2p +1)=1.
D'ou il existe z de IN tel que : U0U­.. 0U0U (2k) =1 (On a composé z (U)).
Alors tous les nombres pairs de IN vérifient la conjecture de SYRACUSE.
Finalement tous les nombres de IN v¨¦rifient la conjecture de SYRACUSE.

           Par :   BEN KHOUYA  ABDENASSER

tu ne pourrais pas mettre un schéma, c'est dur à lire. par exemple, où sont les points M,N, E, F, G, H,...

D'autre part, il y a sans doute quelque chose qui coince car la trisection est impossible à la règle et au compas. De même que la duplication du cube et la quadrature du cercle.

Quelques problèmes dans la démonstration:
"le nombre des points d'arc (ef) =  le nombre des points d'arc (gh)". Un arc à un nombre infini de points. On ne sait donc pas combien il y en a et donc on ne peut pas faire d'égalité.

"soit (z) le nombre de ces points , z est un entier naturel fini (l'arc materiellement est une succession des points (atomes) fini)" FAUX, z, s'il existe est un entier naturel infini

je veux votre preuve

si vraiment l'arc a une infinite de points on peut rassembler ces points en des ensembles finis quand va les appeller (point')

pou le tableau de verite:
Son tableau de vérié est :
                f (n)              g (n)           f (n) * g (n)
                   V                    V                 F  
                   V                    F                 V
                   F                    V                 V
                   F                    F                  F

(la difference symetrique)

N'importe quel professeur de mathématique a déjà entendu parler des trois problèmes de constructions impossibles : quadrature du cercle, trisection de l'angle et duplication du cube.
La preuve en a été fournie par Pierre Laurent Wantzel en 1837. Allez faire un petit tour sur Wilipedia pour vous en convaincre.

Votre démonstration se base sur le paradoxe du tas de sable : "un tas de sable moins un grain de sable égale un tasde sable. Si je répète l'opération un grand nombre de fois, j'obtiens un grain de sable et il équivaut à un tas de sable."

un arc a un ensemble infini de points. je pourrais donc rassembler une INFINITE d'ensemble fini

***

édit Océane

dans la nature  la matiere est fini

on coincide avec tout atome un point c'est tout

petite question qui n'a rien à voir : je peux savoir votre profession?

en plus la methode est verifie experimentalement

***
aurevoir

édit Océane : pas d'adresse mail dans les messages, merci

Vous auriez du publier cette "soi-disant" affirmation un 1er avril. Au moins on aurait rigolé.

Vous devez certainement être déçu d'avoir échoué à votre bac (à sable) spécialité comptage par zéro

Message perso aux modérateurs : connaissiez-vous le zigomar qui s'amuse à vouloir révolutionner la géométrie élémentaire?
Où alors je me demande où se cache la caméra?

J'interviens comme un cheveu dans la soupe, mais c'est quoi ce sujet sur la trisection de l'angle? Du délire pur et dur. Oups, je fais du multi-post. Sorry, je m'en vais

*** message déplacé ***

Bonjour,

ce qu'il y a de tirre-bouchonnant dans ces histoires de trisection d'angles, c'est que ceux qui s'excitent encore là-dessus n'ont même pas compris l'énoncé exact du problème, ou qu'il n'en ont même pas connaissance :
ils en restent à une question posée imprécisément, qu'ils connaissent approximativement par ouï-dire, contrairement à la définition extrèmement précise que les Grecs Anciens ont données de la  " construction à la règle et au compas ".
En effet, parler de "trisectionn de l'angle à la règle et aucompas" est un raccourci faisant oublier des règles très précises et restrictives qui définissent précisément ces instruments et leurs conditions d'utilisation, règles édictées selon les Grecs Anciens.
Si ceci est imparfaitement connu et si ces règles ne sont pas toutes respectées (volontairement ou non), il n'est pas dificile de trouver de nombreuses façons pour réaliser "la trisection de l'angle". On a même donné un nom à ces constructions biaisées : "neusis constructions" et un grand nombre sont décrites dans la littérature.
Les "inventeurs" de nouvelles constructions seraient bien inspirés de faire un tant soit peu de recherche bibliographique, qui leur apprendrait beaucoup, au lieu de perdre leur temps en vaines spéculations ou en ré-inventant ce qui est connu de longue date.
A titre d'exemple, une astucieuse "trisection de l'angle" (qui, évidemment, ne respecte pas toutes les conventions des Grecs Anciens) est présentée en page jointe.

  

Je trace à la latte un angle quelquonque, de sommet A.
Je défini au compas un segment AB, puis BC=AB, puis    CD=BC=AB.
Je trace au compas un cercle de rayon AD qui coupe les demis droites de l'angle en E et D.
A partir de E et D sans changer l'écartement du compas, je trace la bissectrice de l'angle qui passe donc par F, le point d'intersection des arcs de cercles ayant servis à tracer la bissectrice.
Je trace la perpendiculaire à la bissectrice passant par F ( au moyen qu'il vous plaira ).
Je reporte AB en FG sur cette perpendiculaire et :
AG COUPE L'ANGLE EN TROIS !!!

Bonjour et merci !

Bonjour lecteur indulgent,
il est possible que cette trisection ne soit possible que sur des angles quelquonques, mais compris entre 45° et 90° (lesquels sont enfantins à couper en trois).
Pour des angles supérieurs ou inférieurs à cette fourchette, il conviendra donc de les diviser ou multiplier par deux, voire quatre le cas échéant.
Voilà, merci et à bientôt....

Mon cher Triplemad !!!

Je vais être indulgent, et me contenter de dire que tu as "presque" tout faux.
Avec indulgence, j'ai ajouté "presque" pour indiquer que ta méthode , bien que non rigoureusement exacte, est quand même approchée (grossièrement).
Un calcul simple, que tout un chacun peut faire, donne les résultats suivants, par exemple pour quelques valeurs de l'angle A :
A = 90° ta "trisection" donne 31,7° au lieu de 30°
A = 81° elle donne 28,1 au lieu de 27°
A = 75° elle donne 25,6 au lieu de 25°
A = 60° elle donne 19,1 au lieu de 20°
A = 51° elle donne 15,0 au lieu de 17°
A = 45° elle donne 12,3 au lieu de 15°
Elle ne donne le résultat exact que pour un angle de A=68,33 degrés environ, soit 22,77...
Je te signale, puisque tu ne sembles pas le savoir, que de nombreux auteurs ont trouvés depuis fort longtemps des trisections APPROCHEES bien meilleures que la tienne, qui est l'une des moins précises que j'aie vue. ET j'en ai vue "des vertes et de pas mûres", comme on dit !
Il en existe même de très simples. Par exemple celle qui est décrite dans le magazine QUADRATURE n°52, page 4 : elle donne le tiers d'un angle quelconque avec une précision meilleure que 1/100 de degré ( en théorie, car en pratique, l'épaisseur des traits estompe cette précision). Et le lecteur y est clairement averti qu'il ne s'agit pas d'une méthode de trissection au sens correct de ce terme, mais d'une méthode approchée de division par trois des angles. Nuance, nuance... Lorsqu'on parle, il faut être précis et clair dans les mots que l'on emploie.
En effet, lorsqu'on parle du problème de la trisection d'un angle, on ne parle évidemment pas de méthodes de "trisections approchées", puisque de très nombreuses méthodes et souvent astucieuses, sont connues depuis lontemps. Le problème dont on parle est celui de la trisection EXACTE. Alors, par pitié, ne confondons pas tout !!!

Bonjour et merci pour tes informations, mais pardonne moi de revenir là-dessus: les écarts que tu me donnes sont bien supérieurs à ce que la grossièreté des traits pourrait induire d'erreur.
Or, en établissant ma trisection, puis en traçant la bissectrice de l'angle restant, je peux vérifier sans problème que ma premiere trisectrice est bien la bissectrice de l'angle intermédiaire.
Pour être plus clair, chaque demi-droite crée est la bissectrice de l'autre avec  les demi-droite de l'angle de départ.
Comment expliques-tu cela, s'il te plait ?

Bonsoir à tous

Triplemat > pour s'en apercevoir, il suffit d'un peu de géométrie élémentaire (relations métrique dans un triangle, etc ..)... et du cher ami Maple !

Dans le dessin ci-joint, on essaie de trouver une relation entre l'angle initial (que l'on note a) et l'angle supposé être le tiers du premier (que l'on note b).



Pour cela, on exprime l'aire du triangle AGH de deux manières différentes.

Avant tout, on commence par calculer certaines longueurs en fonction de AB, a et b (où a est l'angle initial et b).

Par construction, on a AD=AE=EF=DF, donc ADFE est un losange. En particulier, ses diagonales se coupent en leurs milieux et sont perpendiculaires, et donc (ED) et (IH) sont parallèles.
Ainsi, d'après le théorème des milieux appliqué au triangle AFH, on en déduit que ED=FH.

le triangle AJE est rectangle en J et le triangle ADE isocèle en A, donc on déduit la relation :
Ainsi,

Dans le triangle AFH rectangle en F, on déduit la relation :


Enfin, dans le triangle AFG rectangle en F, on utilise Pythagore :



D'où



On peut donc maintenant calculer exprimer l'aire du triangle AGH.

1ère expression de l'aire : calcul de l'aire avec la formule

on a alors



2ème expression de l'aire :



En égalisant les deux expressions et en simplifiant, on aboutit à :



En somme, si la construction que tu proposes était la bonne, cette équation serait vérifiée en remplaçant b par a/3, et ce pour tout a.
Cependant, ce n'est pas le cas. Regarde ce que trouve Maple.



Maple trouve alors des solutions mais bien sûr seules les solutions réels nous intéressent.
Mises à part les deux premières qui désignent les cas triviaux (le cas où l'angle est nul), il semblerait donc, comme l'a affirmé JJa, qu'il n'y ait qu'une seule valeur précise pour laquelle la méthode marche (même si c'est vrai qu'on ne trouve pas la même valeur, pour ce cas exceptionnel, mais bon, ça c'est une autre histoire).

Kaiser

Bonjour Kaiser,

je te signale une petite erreur dans l'une de tes formules :
Dans A=(1/2)AF*GH tu as oublié le terme cos(a/2)
Une fois la correction faite, nos résultats sont identiques.
De mon coté, j'avais fais le calcul purement trigonométrique, qui est tout à fait élémentaire. Il donne la formule finale suivante (elle coincide exactement avec la tienne après quelques transformations dans la forme des écritures):

Bonjour Triplemat,

dans ton post du 31/10/2007 à 01:51, tu me pose la question : Comment expliques-tu cela, s'il te plait ?
Et bien cela s'explique d'une façon bien simple : des descriptions confuses et une non-rigeur mathématique.
Par exemple tu écris :
"Pour être plus clair, chaque demi-droite crée est la bissectrice de l'autre avec les demi-droite de l'angle de départ."
Cette phase est ambigue : une demi-droite ne peut pas être une bissectrice d'une autre. Cela n'a pas se sens. Emploie le vocabulaire mathématique correctement pour qu'on puisse comprendre ce que tu veux dire sans risque de malentendu.
Ceci dit, je n'en suis pas surpris du tout. Je l'ai constaté à de multiples occasions lors de discussions avec des personnes qui proposent des solutions pour la trisection d'angle ou à d'autres problèmes du même genre. Il est quasiment impossible d'avoir une discussion saine et claire avec ces personnes qui s'exprimment avec autant d'appoximations dans leur langage que dans leur démarche mathématique. Généralement, cela dégénère en un dialogue de sourds qui fait perdre son temps à tout le monde.
Etant habitué à cela, j'ai décidé de ne donner qu'une ou deux réponses au début, puis de ne plus rien répondre, quels que soient les questions posées par la suite.
Ainsi donc, je ne donnerai aucune suite à tes éventuels futurs posts.  
Note bien que tout ce que j'ai dit n'est d'aucune façon péjoratif. Je trouve très bien que des personnes soient intéressées par des recherches mathématiques, quel que soit leur niveau. Je les engage à progresser dans la connaissance des problèmes qu'elles abordent, par un travail personnel d'études de ce qui a été fait sur le sujet et d'une façon plus large, par un accroissement de leurs connaissances mathématiques en général.
Bon courage et bon travail.

Bonjour JJa

Effectivement, j'ai mal recopié mon brouillon (du coup, il y a un décalage entre l'équation résolue par Maple et celle écrite juste avant, mais bon le principal c'est que l'on aboutit au même résultat ! )

Oui, bien sûr !
mon post du 31/10/2007 à 08:58 répondait à celui de Triplemat du 30/10/2007 à 22:30.
Quand on est déjà dans les embrouillaminis, on en rajoute encore !!!

APPREND A LIRE !!!!!!
D'autant plus que même ce que  TU écris, tu ne sais pas le lire...
Une demi-droite ne peut pas être la bissectice d'une autre (bien vu Sherlock)auusi avais-je écris (et toi ré-écris) "bissectrice des demi-droite de L'ANGLE DE DEPART !
Cela dit sans rancune, je cherche encore.
Parce dire que la trisection est impossible, c'est de la foutaise, ce qui est dur, c'est de trouver une méthode commune à tous les angles, parce que trouver une methode pour unn angle donné, rien de plus simple ...
Et au revoir, cher ami

Peux-tu aller voir à "la dupilcation du cube" ?
Et sur la feuille, lire [AH]3/ 2 = [AB]3 ?, l'énnoncé est bon lui...
mercid'avance (section "pas de description")

Salut mon cher Triplemat,

il y a un article qui pourait t'intéresser à l'adresse suivante :
http://les-mathematiques.u-strasbg.fr/phorum5/read.php?8,410762,410762#msg-410762

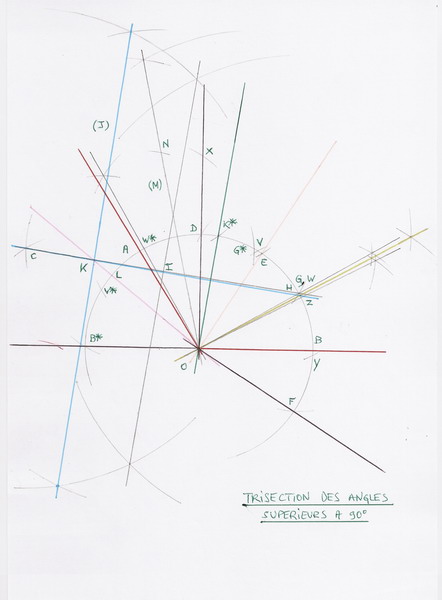
Re, JJA, je tiens à te dire que je te propose dès ce soir un e trisection euclidienne valable pour les angles (en deux parties complementaires : 1. pour ceux egaux ou inférieurs à 90°, 2. pour ceux égaux ou inferieur à 180°)
Attention je developpe la méthode pour que des la sixieme on puisse la reproduire, mais elle est laborieuse, et donc la description encore plus...

ET ELLE MARCHE !

Notez qu'en prolongeant {OB]et {OE] au delà de O, cela permet d'en tracer les perpendiculaires en plaçant la pointe du compas sur le point O, de tracer un arc de part et d'autre sur chacune des demi-droites, puis de tracer les médiatrices des segments ainsi obtenus. Dans ce cas le 2-de la section I passe dans la section préliminaire et les 3-4-5- de la section I viennent s'insérer au début de la secdtion II ne reste plus alors que dans la section I que 1-3- et 6-


SECTION PRELIMAINAIRE

Soit un angle quelconque de sommet O

SECTION I

pour laquelle il est important de conserver tout du long l'écartement du compas servant à tracer le cercle de centre O

     I- tracer un cercle de rayon quelconque et de centre O; il coupe les demi-droites de l'angle en A et B.

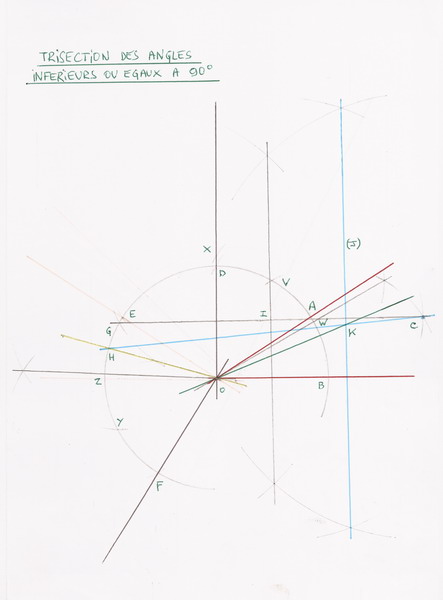
TRISECTION DES ANGLES INFERIEURS OU EGAUX A 90°

Notez qu'en prolongeant (OB] et (OE] au delà du centre O cela permet d'en tracer les perpendiculaires en plaçant la pointe du compas sur le point O, de tracer un arc de part et d'autre sur chacune des demi-droites puis de tracer les médiatrices de chacun des segments ainsi obtenus.
Dans ce cas le 2- de la section I passe dans la section préliminaire et les 4- et 5- de la section I s'insèrent au début de la section II. Ne reste plus donc dans la section I que les 1-3-6.
Dans le cas contraire :

SECTION PRELIMINAIRE

Soit un angle inférieur ou égal à 90° de sommet O

SECTION I

Pour laquelle il est important de conserver tout du long l'écartement du compas servant à tracer le cercle de centre O.

   1- Tracer un cercle de rayon quelconque et de centre O ; il coupe les demi-droites de l'angle respectivement en A et B.
   2- Tracer [OD) la demi-droite perpendiculaire à [OB] au delà du point A.  Pour cela , placer la pointe du compas sur le point B, tracer l'arc en direction ou au-delà du point A qui coupe le cercle au point V ; placer le point W, intersection de la bissectrice de VÔB avec le cercle ; placer la pointe du compas sur le point W et tracer l'arc au-delà du point V qui vient couper le cercle au point D.
   3- A partir des points A et B, tracer les arcs servant à tracer la bissectrice de AÔB (il est inutile de la tracer) ; ils se croisent au point C.
   4- Tracer (OE] de telle sorte que [OD) soit la bissectrice de EÔA. Pour cela placer la pointe du compas sur le point A ; tracer l'arc qui vient couper [OD) au point X ; placer la pointe du compas sur le point X et tracer l'arc qui vient couper le cercle au point E.
   5- Tracer [OF] le segment perpendiculaire à (OE] (même méthode que pour [OD) via les points Y et Z) qui coupe le cercle au point F.
   6- Placer la pointe du compas sur le point D et tracer l'arc en direction ou au-delà du point E qui vient couper le cercle au point G.




SECTION II

Pour laquelle l'écartement du compas peut être variable pour s'adapter à la figure à réaliser et à la taille du support à dessin.

   1- Tracer [OH] la bissectrice de DÔF qui vient couper le cercle au point H
   2- Tracer le segment [GC].
   3- Tracer la médiatrice de [GC] qui vient couper [GC] au point I
   4- Tracer (J), la médiatrice de [IC].
   5- Tracer le segment [HC] qui coupe la droite (J) au point K.
   6- Tracer la demi-droite  [OK).

NOTE

Pour les angles de 90 ° [OA], [OD) et [OE] se superposent et [OF] n'est autre que le prolongement de (OB] par delà le point O.

:

AÔK fait le tiers de AÔB.

.

Ceci complète voire remplace partiellement la methode decrite précedemment (des angles inférieurs ou égaux à 90°)

      NOTES (A insérer)

En prolongeant (OB] au delà du point O le 2 bis -disparaît.

      SECTION I  (A insérer)


2 bis- tracer [OB*] le segment perpendiculaire à [OD) (même méthode que pour [OD) via les points V* et W*) qui coupent le cercle au point B*
3- Le point C est le point d'intersection des arcs servant à tracer la bissectrice de l'angle B*ÔA.
4-5- Faites la trisection de l'angle BÔK ; pour cela  utiliser la méthode de trisection (ci-avant) des angles inférieurs ou égaux à 90° pour placer le point K.
6 bis- Placer la pointe du compas sur le point A et tracer l'arc en direction du point B qui vient couper le cercle au point G*.

       SECTION II (A insérer)


6- Tracer [OK]qui vient couper le cercle au point L.
7-  Tracer la droite (M), bissectrice de l'angle LÔG*.
8-  Placer la pointe du compas sur le point A ; tracer l'arc qui vient couper la droite (M) au point N ; placer la pointe du compas sur le point N et tracer l'arc qui vient couper le cercle au point K*
9- Tracer [OK*).

AÔK* fait le tiers de AÔB.