Bonjour badzi

Dans le cas général, il me semble que c'est impossible ! (ça a été démontré !)

Kaiser

Bonjour badzi,

Avant d'éventuellement te répondre , je veux être certain de bien comprendre ta question.

S'agit-il de diviser, par le dessin (avec latte et compas), un angle quelconque en trois parties égales ?

Merci de me répondre.

atomium.

Bonjour atomiun.
Il s'agit de diviser un angle sur 3 par la règle rt le compas.C'est possible car j'ai réussi à le diviser mais je cherche une démonstration.
Si tu trouve une méthode avec la démonstration poste la moi s'il te plait

Re-bonjour badzi,

Bien reçu ta réponse.

Je regrette de ne pouvoir t'aider. Je n'ai pas la démonstration.

atomium

Bonjour à tous

badzi> juste pour voir. Quelle est ta méthode pour diviser un angle quelconque en 3 parties égales ?
En effet, ceci me paraît bizarre car il a été démontré qu'on ne pouvait faire ça que si la valeur de l'angle vérifiait certaines propriétés.

Kaiser

Bonsoir à tous

Sachant que 1/3 = 4/12, ne serait-il pas possible de diviser l'angle en deux, puis en 4 c'est à dire diviser chaque moitié en 2), en 6, et enfin en 12 ? Chaque "groupe" de 3 angles adjacents en partant du côté de l'angle de départ serait alors un tiers de l'angle.

Je ne sais pas si ce que je dis est très clair

Estelle

Bonjour kaiser,

Je vois ta demande adressée à badzi, visant à connaître sa méthode pour diviser un angle quelconque en 3 parties égales.

Je ne conais pas la méthode de badzi, mais te voyant dubitatif, je me fais un plaisir de te donner la mienne.

L'image, faite avec le logiciel GéoGébra, n'est pas très lisible; j'ai dû fortement la réduire pour pouvoir l'attacher dans la fenêtre-réponse .Le cas échéant,si tu le souhaites, je puis t'envoyer une image plus grande jointe à un email.

Ci-dessous l'explication de la construction:

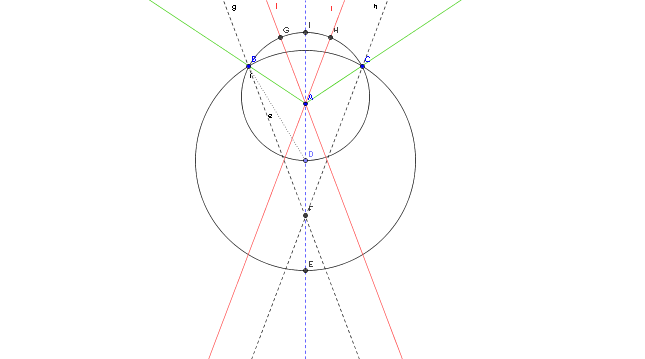
l'angle quelconque à diviser en trois parties égales est représenté par son sommet A et par ses côtés de couleur verte.

Procédé:

- construire la bissectrice de l'angle;
- de A comme centre, tracer un cercle quelconque, coupant  
  les côtés de l'angle en B et C, et la bissectrice en D;
- de D comme centre, avec DB comme rayon, tracer un cercle
  coupant la bissectrice en E;
- joindre F, milieu de ED, à B et C  pour obtenir les
  droites g et h ;
- par A, mener les parallèles à g et h;
- ces parallèles, représentées en rouge, divisent l'angle
  initial en 3 angles égaux, soit BAG = GAH = HAC.

Comme je l'ai dit à badzi, je ne puis en faire la démonstration. Si tu y arrives, veux-tu bien me la faire connaître. Grand merci.

atomium

Bonjour à tous.

Je vais apporter de l'eau au moulin de Kaiser .
Il me semble bien en effet que le problème de la trisection d'un angle (quelqconque) à la régle et au compas est rigoureusement impossible (et ceci à été démontré)

Je confirme, la trisection d'un angle à la règle (non graduée) et au compas est impossible.
Il existe une multitude de méthodes pour approcher cette trisection mais ce ne sont que des approximations.

Bonjour,

Loin de moi l'idée d'insister, je me doute que vous avez tous raison sur le fait que la trisection d'un angle à la règle et au compas est impossible. Cependant, je ne comprends pas ce qui ne marche pas dans ma méthode de 20:40 :

Sachant que 1/3 = 4/12, ne serait-il pas possible de diviser l'angle en deux, puis en 4 c'est à dire diviser chaque moitié en 2), en 6, et enfin en 12 ? Chaque "groupe" de 4 angles adjacents en partant du côté de l'angle de départ serait alors un tiers de l'angle.



Merci.

Estelle

STL, si il est impossible de diviser un angle en 3 à la règle et au compas, il est aussi impossible de diviser un angle en 6.

Tu ne peux donc pas te servir d'une division impossible à réaliser (par 6) pour montrer qu'on peut diviser un angle en 3.

On peut facilement diviser un angle par une puissance de 2, soit par 2 , 4 , 8 , 16 ... mais pas par 6 , 12 ...

Pour celui que cela intéresse:

OK merci J-P

Estelle

Bonsoir à tous

Merci d'avoir confirmé ma réponse.
atomium>Je pense savoir ce qui cloche dans ta construction. Ce n'est pas forcément très voyant, mais il me semble, que si les 3 angles étaient égaux, alors une droite rouge et une droite en pointillé qui se coupent doivent se couper exactement sur le cercle ce qui ne me semble pas être le cas.

Kaiser

Je me suis penchée sur la question ce matin.
Il y a une méthode très simple pour faire une trisection d'angle...
Soit un angle BAC délimité par les côtés AB et AC.
Tracer l'image des points A, B et C selon une translation de vecteur "-->AB/2" (désolée pour la notation).
Par commodité d'écriture :
A -> A'
B -> B'
C -> C'

Tracer [AC'). Bravo, vous venez de diviser l'angle BAC en 1/3 - 2/3 (divisez l'angle "C'AB" en deux, si vous voulez en être sûr).

Cette méthode très simple découle d'une démonstration vectorielle.


Un mélange de "proportionnalité" et de le principe selon lequel :
Soit une cercle de diamètre AB, de centre 0.
Soit M un point quelconque du cercle
L'angle "MOB" = 2 fois l'angle "MAB".
Remarque : le vecteur "-->OA"=1/2 vecteur "-->AB"
Il suffit de faire une construction géométrique avec une proportion 1/3 au lieu d'1/2

Donc, c'est tout à fait du niveau mathématiques de classe de 5ème.

)
Les mathématiques, c'est fait pour rêver...

NOTA BENE :
1/ il faut absolument que AB=AC (d'où l'importance du compas !).


2/ Je vais tester avec d'autre valeur (1/12, 1/5, et pourquoi pas 1/29 ?). D'après la logique utilisée, c'est sensé fonctionner. A tester, donc.

3/ J'attends vos retours... :-p

Septusection - ok
pentasection - ok
nonasection (?)- ok
en 11 sections d'angles égaux : ok
...
Un peu désespérée... J'ai envie que ça se sache, que ça marche. N'en déplaise à Galois !

D'autant plus que cela ne constitue en rien une avancée technologique, ni une révolution mathématique... Où est le scandale ?!!!

Tout cela me semble bien faux.

Supposons que
Alors
Soit l'angle .
Soit l'angle .
On veut montrer que

Dans le triangle ACC' :


Or :





Donc :



Et cette expression n'est pas du tout égale à

Sauf erreur.

Nicolas

Je vous remercie énormément de votre contribution...
A force de tester et retester ma méthode, à force d'entendre "galois a démontré... Je l'ai étudié... Je ne veux même pas voir ta construction...", je n'ai qu'une envie : qu'on me démontre que ma construction est fausse.

Toutefois, en essayant de reproduire votre démonstration, je butte sur un premier point :

1/ Pouvez-vous développer, d'un point de vue géométrique, sin CAC' et sin ACC' ?

Petit développement fait de mon côté :
sin (C'AC)/CC' = sin (ACC')/AC'
ssi
AC'.sin (C'AC) = CC'.sin (ACC')
Cela revient à démontrer :
AC'.sin (C'AC)= CC'.sin (pi-ACC')

Vérification de cette égalité :

a/ Construisons AC'.sin(C'AC)
Soit CH la hauteur du triangle ACC'.
sin CAC' = CH/AC
On construit le point F tel que AFC'=ACH
AC'.CH/AC = FC'

b/ Construisons CC'.sin (pi-ACC')
Soit GC' une hauteur du triangle CFC'.
CC'.sin (pi-ACC') = CC'.sin (FCC')
                  = CC'.GC'/CC'= GC'

Sauf cas particulier, les points G et F ne sont pas confondus.
donc,
sauf cas particulier,
FC' différent de GC' et
sin (C'AC)/CC' n'est pas égal à sin(ACC')/AC'

Merci encore infiniment pour cet élément de démonstration que vous avez proposé, et s'il vous plaît, continuez à chercher !

Bonjour,

Je ne comprends pas bien ton message.

1. Si tu me demandes pourquoi ,
tu trouveras des éléments de réponse ici :
relations métriques dans le triangle proposition 7 (ii)

2. Si tu veux savoir pourquoi ta démonstation du 6/6 15h18 ne me convaint pas...
En fait, tu n'as rien démontré. Tu as juste écrit : "Il suffit de faire une construction géométrique avec une proportion 1/3 au lieu d'1/2". Cela ne constitue par une démonstration.

Nicolas

Bonsoir,

Grande nouvelle, grâce aux apports de Nicolas_75, j'ai enfin pu me lancer dans des calculs.
Au final, effectivement, ma construction, si elle tient la route sur une figure géométrique, n'est pas une trisection d'angle au sens précis, algébrique, trigonométrique du terme.

J'obtiens une erreur d'angle comprise entre 0.0058° pour un angle de 1°, à une erreur de 1° (!!!) pour un angle à 90°.


Sur un angle aigu "moyen", l'erreur ne se voit pas. D'autant plus que la précision des instruments reste limitée (un trait de crayon fait entre 0,1 et 0,3 mm, à vue d'oeil).
Quelques valeurs d'erreur arrondies au 10000ème obtenues par calcul
angle de 60° - erreur 0.43301 °
angle de 30 ° - erreur 0.18301 °
angle de 45° - erreur de 0.24167 °

Donc, géométriquement, avec les instruments standard, sur une feuille A4, oui, "ça passe". Par contre, au niveau trigonométrique ou simplement en changeant d'échelle, ça crée des erreurs assez facheuses...

Je garde la méthode sous le coude, au cas où un jour je voudrais faire des mosaïques à partir d'un carré de faillance...

Bonjour,

au sujet de l'antique problème de la trisection de l'angle, à la règle et au compas, un article est disponible à :
http://les-mathematiques.u-strasbg.fr/phorum5/read.php?8,410762,410762#msg-410762

atomium a fais une grosse erreur dans son dessin, on vois clairement que l'angle n'est pas divisé en trois partie égal puisque l'angle "externe" n'est pas correctement divisé, il s'agit donc d'une approximation.

Un grand nombre de méthodes ont été publiées pour diviser APPROXIMATIVEMENT par trois un angle quelconque. Certaines sont très simples et extrèmement précises, beaucoup plus précises que ce qui a été indiqué dans certains des messages précédents.
Tout ceci n'a plus grand intérèt maintenant, par rapport à tout ce qui a été trouvé depuis longtemps.
Voir quelques exemples connus, de niveau élémentaire, dans l'article "Trisection", par le lien :
http://www.scribd.com/JJacquelin/documents

Bonjour JJa

Cela ne te rappelle rien ceci ? :

C'était l'époque où on recevait des menaces de "..." de se faire intenter un procès pour "pillages des idées" de ce "..."

Salut, J-P
avec mes cordiales salutations à cette occasion !
Bien sûr que les anciens s'en souviennent...  

bonsoir,

je n'ai aucune idée sur la question, mais je trouve que cette question et les réponses apportées ne sont en aucun cas du niveau d'un 5ème!!!