Bonjour,

Salut Greg

A mon avis ça veut dire que le plan est "tangent" au cercle défini par l'intersection du cône et de z = h (la hauteur en question).

Moi ce que je ferais c'est tout d'abord déterminer l'équation d'un tel plan incliné (il n'y en a pas qu'un mais le problème est invariant par rotation autour de Oz).

Ensuite l'intersection se traduit par un système, et si tu te places dans un repère orthonormé lié au plan tu peux déterminer l'équation de l'ellipse et donc trouver les valeurs des demis axes.

Au passage ça fait fortement penser au théorème belge.

J'ai mis une image en pièce jointe pour montrer ce que je connais. La longueur des 2 segments verts je sais les calculer par intersection entre l'équation des segments et du cône. Maintenant ces 2 segments ne sont PAS les demi-axes de l'ellipse car ils se coupent au centre du cone et non au centre de l'ellipse, donc comment trouver l'air de cette surface ?

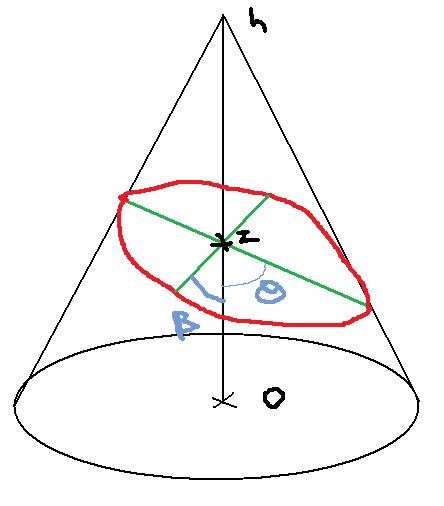
S'il te suffit de trouver la valeur des 1/2 axes, ce sont la longueur
des segments verts divisée par 2, à condition de déterminer ces segments
selon les conditions suivantes :
- le grand axe étant la ligne de plus grande pente du plan (P).
- le petit axe étant la droite horizontale, médiatrice du grand axe.

...

oué le grand segment vert c'est bien le grand axe, maintenant le petit segment n'est pas le petit axe, après je suis d'accord qu'il faudrait prendre la moitié du grand axe et prendre le segment qui passe par ce centre. Mais c'est du bricolage fait avec les mains. En plus en y réfléchissant un peu c'est pas si trivial de trouvé la longueur du petit axe, parce que moi je connais l'équation du coté du cône de révolution.

qui a dit que c'était trivial ? et du bricolage avec les mains ?

fais une coupe verticale du cône passant par son axe.
intersection de la droite de plus grande pente avec les 2 génératrices --> point A et B du grand axe.
I milieu de [AB], puis intersection de la droite horizontale passant par I avec les 2 génératrices --> point C et D --> petit axe = d(C, D)

...

ça va c facile pour le point A et B (c'est ce que j'ai déjà fais), le problème c'est que pour le point C et D, je peux pas faire une coupe qui passe par l'axe du cône et du coup ma fonction de génératrice n'est plus bonne enfin j'ai y réfléchir un peu je reviendrais plus tard

c'est cela...

...

Re

En fait d'après une source extérieure ça peut se faire géométriquement :

L'excentricité est donnée par avec l'angle au sommet et l'inclinaison du plan.

Ca permet de trouver facilement le grand axe et d'en déduire le petit axe via la relation où .

ah oué c'est cool car comme je connais deja a, et c'est vite fait d'avoir b, le problème est que j'ai un autre angle d'inclinaison du plan ...

après peut être qu'un plan doublement incliné ne forme plus une ellipse ...

l'intersection d'un plan convenablement incliné et d'un cône ça donne toujours une ellipse

le plus simple peut être c'est d'effectuer un changement de base
prendre comme nouvelle base où sont de norme 1 porté par les axes vert sur le dessin et

mais attention cette nouvelle base n'a aucune raison pour être orthogonale
si on note x',y',z' les nouvelles coordonnées dans cette nouvelle base on peut écrire (en théorie, ce ne doit pas être utile de le faire en pratique) l'équation du cône
et les équations de l'ellipse seront alors
celle du cône et z'=0
par chgt de base on revient dans la base canonique orthonormée avec l'équation du cône initiale
on obtient deux equations et l'on doit en eliminant z pouvoir en retirer une seule equation du second degré forme quadratique en 2 variables
pour trouver les longueurs des axes, il faut diagonaliser (calculer valeurs propres et vecteurs propres) la matrice de la forme quadratique ds une base orthonormée

pour comprendre tu peux lire
avec acrobat tu peux le parcourir il y a un paragraphe sur les directions principales des quadriques avec un exemple simple d'ellipse

la pour le coup, c'est plus des maths fait avec les mains, c'est intéressante de résoudre le problème de cette manière, j'vais essayer de prendre le temps de me pencher dessus. merci apaugam et  infophile pour vos réponses précieuses et merci aux autres pour leur contributions

Pour poursuivre sur l'idée d'infophile,
ce qu'il nous manque ici, c'est l'inclinaison du plan.

Si l'on admet que l'on connaisse les inclinaisons et selon deux plans orthogonaux
(peut-être les droites figurées en vert ici), on peut en déduire l'inclinaison générale :

   tg() = tg() tg() / (tg²() + tg²())

...

t'essaye de calculer l'angle équivalent à theta + beta ? pcq moi je connais tout les angles que ce soit du plan définie par les 2 droites verts ou le cone

Bon, j'ai pas trop le temps actuellement de me pencher sur la grosse demo, et faut que j'ai des résultats. En reprenant mon ellipse je me suis rendu compte que je connaissais plutôt les grandeurs vertes. Mais je pense pas qu'il y ait plusieurs ellipses qui puisse passer par les 4 points rouges.
Donc normalement en connaissant les coordonnées de ces points on doit pouvoir obtenir tout les paramètre de cette ellipse, c'est a dire a,b,c,F,F'.

En fait, on peut aussi facilement trouver le centre de l'ellipse, c'est les coordonnées ((a+A)/2,(b+B)/2)

bon enfait ça va c'est pas dur, laissez tomber, je posterais la réponse pour que ça puisse aider d'autres personnes

PS: c'est chiant ce forum ou on peut pas éditer

Le problème est facile, la résolution est plus chiante.
Voila les solutions, DGA comme demi grand axe et DPA vous devinerez aisément.

Les valeurs a,b,A,B corresponde aux grandeurs que j'ai définie dans l'ellipse quelque posts au dessus (je sais c'est pas malin de les avoir appelé a et b).

Je ne comprends pas bien les données du problème.
Connaît-on l'angle que fait le plan sécant avec l'axe du cône ?
Sinon, comment ce plan est-il déterminé par rapport au cône ?

oui on connait l'angle et l'altitude, il est même incliné selon 2 axes (voir schema vers le debut)

Pourquoi deux angles ?
Le plan sécant fait "un seul" angle avec l'axe du cône, qu'on pourrait caractériser par l'angle (complémentaire) que font la normale au plan et l'axe du cône.
N'est-ce pas ?

2 angles pcq dans mon problème j'ai 2 angles, ça représente l'intersection entre un faisceau divergent et un plan, sauf que ce faisceau et paramétré par 2 angles dans 2 plan perpendiculaire

Bon en reprenant ma géométrie sous catia (c'est plus facile pour voir dans l'espace), je me suis rendu compte que je m'étais trompé. En fait j'ai pas du tout le schéma que d'ellipse que j'ai fais plus haut. Les calculs restent bon quand même dans ce cas, mais c'est pas le mien.

Donc je vous donne des images de ma géométrie:
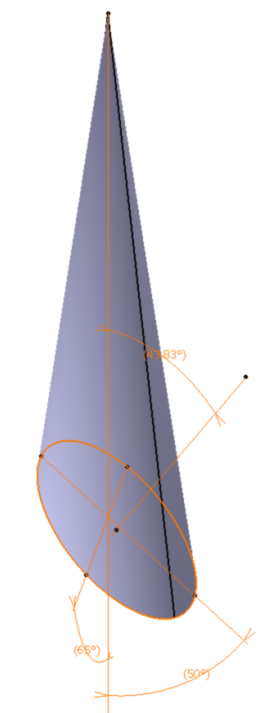
c'est un cône avec un demi angle de 8.607°, le plan coupe son axe à une distance de 295.375 mm du sommet.

1ere image: donne les 2 angles que je connais et l'angle entre la normale au plan et l'axe du cône que je ne connais pas
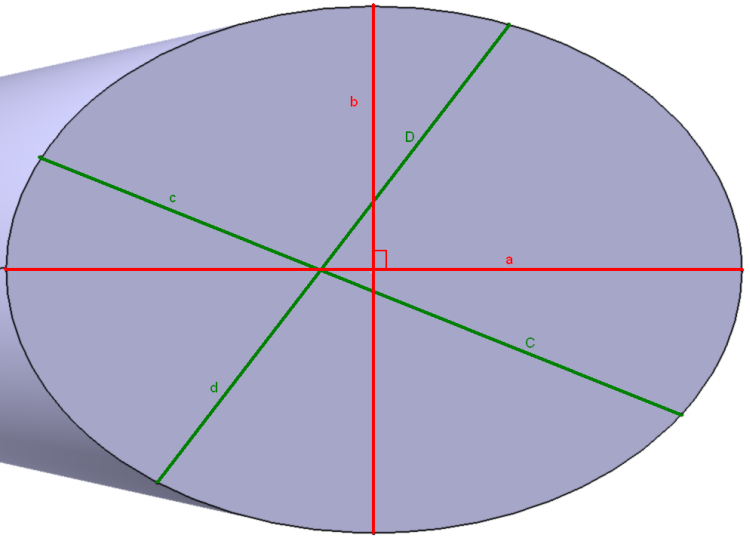
2ème image: Il s'agit de l'ellipse que je cherche, en vert les longueurs que je connais (les 2 axes verts ne sont PAS perpendiculaire) et en rouge ce que je cherche.
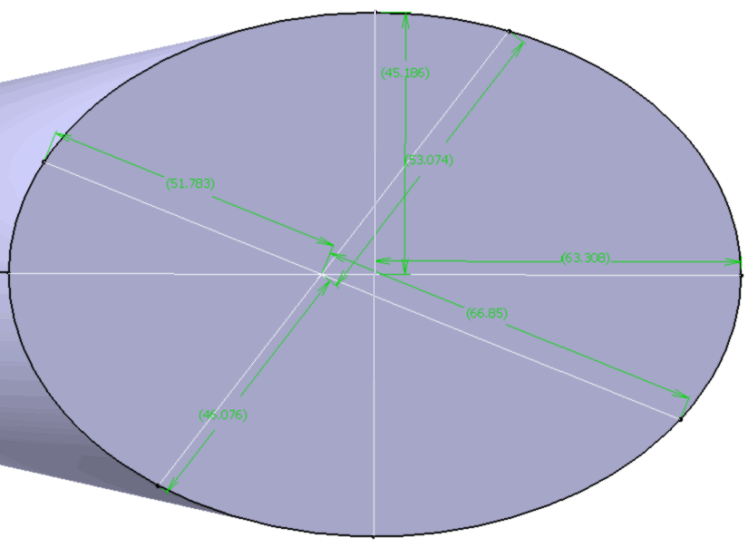
3ème image, les valeurs de toutes les longueurs dans le cas que j'ai pris, pour vérifier numériquement l'expression littérale si on la trouve.

Si l'on peut déterminer la droite de plus grande pente du plan qui rencontre l'axe du cône, les points d'intersection de cette droite avec la surface du cône sont les extrémités du grand axe de l'ellipse section, d'où la longueur de ce grand axe et la position du centre de l'ellipse.
Ensuite, on peut déterminer la position d'un foyer de l'ellipse grâce au théorème de Dandelin, selon lequel une sphère, tangente intérieurement au cône et tangente au plan sécant,a son point de contact avec le plan situé en un foyer de l'ellipse.
La construction peut se faire à plat dans le plan contenant l'axe du cône et le grand axe de l'ellipse.
Cela serait-il utilisable pour la résolution de ton problème ?

"Si l'on peut déterminer la droite de plus grande pente du plan qui rencontre l'axe du cône, les points d'intersection de cette droite avec la surface du cône sont les extrémités du grand axe de l'ellipse section, d'où la longueur de ce grand axe et la position du centre de l'ellipse."

ça on peut, il faut juste déterminer l'angle de la plus grande pente avec l'axe, ce ce que j'essaye de faire, j'ai trouvé
tan()= (tan()+tan())/2 sauf que j'ai pris les angles complémentaire de ceux sur la figure(donc 40° et 25°) et j'obtiens 42.709° alors que lorsque je demande l'angle entre les 2 plans catia me dit 43.83.

"Ensuite, on peut déterminer la position d'un foyer de l'ellipse grâce au théorème de Dandelin, selon lequel une sphère, tangente intérieurement au cône et tangente au plan sécant,a son point de contact avec le plan situé en un foyer de l'ellipse.
La construction peut se faire à plat dans le plan contenant l'axe du cône et le grand axe de l'ellipse."

Ça j'aimerais bien m'en servir mais je sais pas comment m'y prendre, si tu peux m'aider ...  

bon ça y est j'ai en fait c'est tan()=(tan²()+tan²()), je ne sais pas pourquoi, mais ça marche, j'ai trouvé en tâtonnant avec les conditions limites  (c'est la première fois que ça marche).
Du coup je vais pourvoir calculer la longueur du grand axe. Manque encore à savoir comment trouver les foyers, j'aimerais aussi connaitre la position de mes droites vertes par rapport aux rouges (je n'ai pas besoin que de la surface en fait) pour cela je pense que connaitre l'angle entre les droites vertes aiderait fortement

Il suffit de dessiner la coupe de l'ensemble de la figure par le plan contenant l'axe du cône et la droite de plus grande pente du plan.
Ce plan axial coupe le cône suivant deux génératrices et le plan sécant suivant ladite droite, ainsi que la sphère tangente au cône et au plan sécant suivant un grand cercle de celle-ci.
Ce cercle est le cercle inscrit dans le triangle formé par les deux génératrices et la droite précitées, qu'il est facile de construire.
Le point de contact du cercle et de la droite de plus grande pente est l'un des foyers de l'ellipse.