Inscription / Connexion Nouveau Sujet
Trouver l'expression d'une fonction grâce à sa courbe.
[cBonjour à tous,
J'ai eu un DM de Math & je suis bloquée à l'exercice n°2. Je dois trouver grâce aux courbes, l'expression d'une fonction.
Voici l'énoncé :
Charles-Edouard a perdu le texte de son DM, il ne lui reste plus que les courbes représentatives des deux fonctions qu'il doit étudier. Retrouvez pour lui une expression de ces fonctions.
Voici les courbes :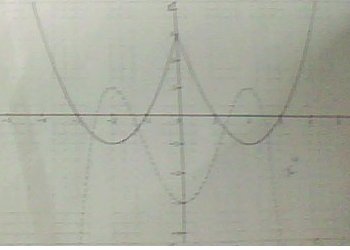
* Tom_Pascal > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois Aphrodite
, merci d'en faire autant la prochaine fois Aphrodite  *
*
Je sais que la seconde courbe est la dérivée de la première & je pense que c'est du degré 4.
Merci d'avance pour votre aide.
Cordialement
Aphrodite.
Bonjour
Es-tu sûr que l'une représente la dérivée de l'autre ?
En voici deux qui correspondent "en gros" à ce qu'on aperçoit.
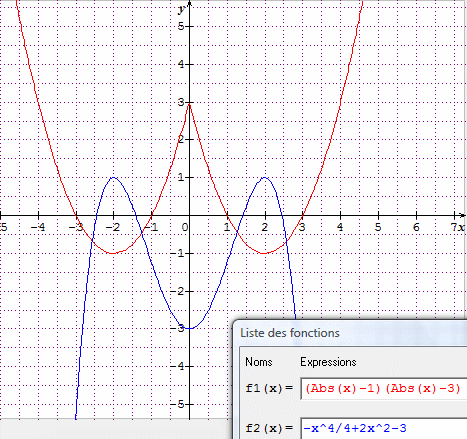
Bonsoir,
Oui, Malou, la seconde courbe c'est celle en pointillée. Et les courbes ressemblent à cela, mais non je ne suis pas sûre que ce soit ça dérivée.
Bonjour Aphrodite,
Je vois que tu as repensé au problème...
effectivement ce n'est pas la dérivée...
pour t'en convaincre, il te suffit d'essayer
tu dis "j'affirme que la bleue est la dérivée de la rouge"et je lis de gauche à droite le dessin...quand la bleue est sous l'axe des abscisses, les valeurs prises sont négatives, et la fonction (rouge ) est décroissante
au moment où la bleue passe au dessus de l'axe, les valeurs sont positives, et la courbe devrait devenir croissante, ce qui n'est pas le cas sur le dessin
donc la bleue ne représente pas la dérivée de la rouge
ensuite tu dis : je fais l'hypothèse contraire, je suppose que la rouge est la dérivée de la bleue...et tu raisonnes de même...
voilà...
Okay, merci.
Mais comment puis je calculer l'expression de la courbe ? J'avais pensé à faire comme une parabole pour chaque "vague" pour ne pas répéter "parabole" avec la formule a(x-alpha)(x-beta) & après me débrouiller avec ça.
Pour ma part je m'étais intéressé tout d'abord à la courbe au "trait épais" : la fonction correspondante semble paire (courbe symétrique par rapport à l'axe des abscisses), non dérivable en 0. Je ne me suis donc occupé dans un premier temps que de la partie "droite" ; cela ressemble à une parabole coupant l'axe des abscisses en x=1 et x=3, donc d'équation y=a(x-1)(x-3). Puisqu'elle coupe l'axe des ordonnées en y=3 j'en ai déduit a=1. Enfin l'histoire de la parité m'a conduit à
f(x) = (|x|-1)(|x|-3)
Pour l'autre courbe, même remarque pour la parité (mais pas de problème pour la dérivabilité). Comme la dérivée s'annule trois fois, sans doute de la forme ax(x+2)(x-2)=ax3-4ax, j'ai donc penché pour un polynôme de degré 4 de la forme
g(x) = ax4/4-2ax2-3 (puisque g(0)=-3)
Et puisque g(2)=g(-2)=1, j'en suis arrivé à a=-1
donc g(x) = -x4/4+2x²-3
Mais bien sûr comme on n'a aucune indication sur la nature des courbes il peut y avoir d'autres démarches conduisant peut-être à d'autres fonctions....
Merci pour ton aide.
Je vais essayer de refaire les calculs tout bête en réalité & mettre cette explication en place pour plus tard au cas où ^^
En tout cas, je te remercie beaucoup.


