Bonjour

dans le cas présent, je ne vois pas à quoi sert la dérivée seconde car on sait étudier le signe de la dérivée 1re....

normalement, dérivée 1re, est ce qu'elle s'annule et quel est son signe

si on n'arrive pas à le faire (pour des raisons diverses), on calcule la dérivée seconde, on étudie son signe et on en déduit les variations de la dérivée 1re, puis son signe, et ensuite les variations de la fonction

Salut,
Il te faut le signe de y'.
et y'=12x³-12x=12x(x²-1)=12x(x-1)(x+1).
Tu peux faire un tableau de signes.

Salut malou  

salut Yzz

Salut

C'est que dans la question on me demande de passer par la dérivée première et ensuite la seconde.

Je comprends vraiment rien à vôtre explication
C'est quoi un tableau de signes ?

ouch

OK!....

y'' = 36x²-12

donc tu vas regarder si elle (cette dérivée seconde) s'annule et quel est son signe
à toi!

donc 0 = 36²-12
12=36x²

donc 12/36 = x²

1/3 = x²

???

Vais aller pleurer un peu et je reviens haha !

Sinon je peux passer comme ça :

0 = 12(3x²-1)
Mais je sais pas qu'elle valeur donner a x pour que ca égal a 0

Ouin je sais que c'est décourageant pour vous, mais je suis vraiment reconnaissante de l'aide que vous m'apporter

1/3 = x²

c'est très bien !....

ce qui donne x=(1/3) ou x=-(1/3)

OK ?

avec ça, et tes connaissances sur les polynômes du second degré, saurais-tu me donner le signe de f''(x)

je ne sais pas trop
Je dirais + car c'est le signe devant x²

?

merci

+ à l'extérieur des solutions

donc

+ 0 - 0 +

et les zéros sont en face des 2 racines que je t'ai écrites...

mais je t'assure que faire la dérivée seconde sur cet exemple est débile....

tu vas devoir calculer f'((1/3)) ainsi que l'autre

alors que la dérivée 1re était toute simple à étudier, comme te l'avait dit Yzz en faisant un tableau de signes.....

Merci

Mais je comprends toujours pas comment ça fonctionne.

C'est quoi le tableau de signes ...

Rendu au point ou nous sommes, j'ai pas trouvé mes maximunms et minimums et les coordonnées.

Tu écris ceci :

+0 - 0 +

Ca vient de quel endroit ?

Oui je sais, je suis une cause perdue

c'est le signe de ta dérivée seconde sur laquelle on vient de travailler
polynôme du second degré, du signe du coeff de x² à l'extérieur des solutions

Merci pour ta politesse à mon égard même si je suis nulle

Vais essayer de chercher comment trouver ma réponse.

Merci beaucoup pour ton aide

mais le imbuvable n'est absolument pas pour toi....
et je vois pas pourquoi tu répètes que tu es nulle....

moi, tout élève qui cherche à comprendre, mérite qu'on lui explique....

alors, par contre, cet exercice est peut-être à un endroit du livre qui te laisse penser qu'il faut faire la dérivée 1re et la dérivée seconde, mais j'aimerais que tu te rallies à mon point de vue, que ce n'est pas ici la méthode appropriée

je ne sais pas si tu as regardé le profil de Yzz et le mien...
et nous sommes tous les deux d'accord....

Merci

J'ai pleinement confiance en vous, vous m'avez aidé plus d'une fois
Mon problème vient du fait que mon tuteur veut que je passe par ces méthodes

Voici la question intégrale :
"trouver le maxima et le mimina de f(x) = 3x⁴-6x² et préciser les coordonnées des points.
Utiliser le test de la dérivée première et de la dérivée deuxième."

Du coup j'essaie de comprendre ce qu'il désire et de comprendre comment y arriver.

Tu as peut être une série d'exercices, pour certains il faudrait faire les 2 dérivées, et pour d'autres non....j'essaie de comprendre....

car je t'assure que c'est une hérésie sur cet exemple là de faire la dérivée seconde....en plus là dessus, cela ne te fait pas comprendre l'intérêt de la dérivée seconde quand elle est nécessaire

tu es en quelle terminale (quelle série?) ? et tu dis que c'est ton tuteur qui veut ça ?....

je reprends l'énoncé
y = 3x⁴-6x²
y'=12x³-12x
y'=12x(x²-1)
y'=12x(x-1)(x+1)
cette dérivée s'annule pour 0, -1, et 1
son signe est - 0 + 0 - 0 + (ça c'est pas dur à montrer)

et donc la fonction va être décroissante, puis croissante, puis décroissante et à nouveau décroissante (on fait le tableau)
et c'est fini

je te mets la courbe

tu me dis s'il faut continuer la méthode avec la dérivée seconde...mais tu me laisseras du temps, car pour réussir à écrire tout ça, je le ferai demain à ce moment là....(je viens de le faire au brouillon.)..

comme tu veux....

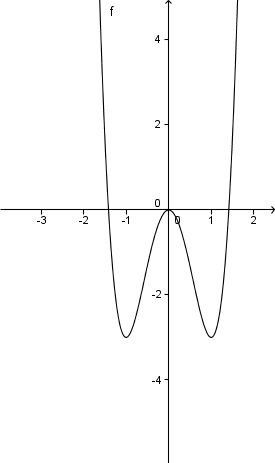
Oui on doit passer par la dérivée seconde aussi.

Je viens du québec, c'est peut être une différence, de plus c'est un cour d'appoint pour les adultes qui désire faire des études universitaires.

Voici, tirer directement de mon manuel :
"On commencera toujours par le test de la dérivée deuxième puisqu'il est plus rapide d'application, le test de la dérivée première obligeant à résoudre des inéquations."

Sur le coup, on me demande toujours dans mes questions de résoudre le tout avec la dérivé deuxieme et la dérivée première par la suite.

C'est compliqué ici haha!!

Donc voila ce que je comprends :

f(x) = 3x⁴-6x²
f'(x) = 12x³-12x
f''(x) = 36x²-12

Test de la dévirée seconde :
0 = 36x²-12
12 = 36x²
x² = 1/3
x = (1/3)
Je sais pas en quoi ca m'aide ...

Test de la dérivée première :
f'(x) = 12x³-12x
0 = 12x(x²-1)
x = 0, 1 et -1

Donc si je remplace f(-1),f(0) et f(1) ca me donne : -3, 0 et -3

Mes minimums seraient : (-1,-3), (1,-3) et mon maximum (0,0)
Bien que cela n'ait pas de bon sens de calculer la dérivée deuxième ... je fais comment pour résoudre le tout si je devais passer seulement par la dévirée deuxième ?

Merci pour tout

Une dernière question concernant ce que tu as inscris :

je reprends l'énoncé
y = 3x4-6x2
y'=12x3-12x
y'=12x(x²-1)
y'=12x(x-1)(x+1)
cette dérivée s'annule pour 0, -1, et 1
son signe est - 0 + 0 - 0 + (ça c'est pas dur à montrer)


=========

Je ne sais pas comment calculer le signe  - 0 + 0 - 0 +
Est-ce que c'est tout simplement en disant x = -2, x = -1/2, x = 1/2 et x = 2 pour trouver si le résultat est + ou négatif avant ou après ces points critiques?
Merci

pour déterminer le signe d'un produit  on étudie le signe de chacun des facteurs et ensuite on applique la règle des signes  

vous pouvez toujours vérifier en prenant certaines valeurs avant après

re bonjour, et bonjour aussi à hekla qui nous a rejoint et t'a envoyé ce magnifique tableau de signes pour te faire comprendre comment ici (en France), nous faisions faire une étude de signes aux élèves...je n'avais pas le courage de te le faire hier soir !....

j'ai compris.....
en réalité, tu ne cherches pas à étudier les variations de f, mais seulement à savoir si la fonction qu'on te donne admet des minimum relatifs ou des max relatifs

alors je suis d'accord

les problèmes de min relatif ou de max relatif sont des problèmes de concavité de courbe (le creux vers le haut ou vers le bas, OK).

et oui, les problèmes de concavité se règlent en regardant simultanément dérivée 1re et dérivée seconde

tu calcules tes deux dérivées (1re et 2nde)
tu cherches les valeurs qui annulent la dérivée 1re
ici x = 0, 1 et -1
tu calcules
f" de chaque valeur

et tu appliques
max en a pour f'(a) = 0 et f"(a)< 0 (car donne concavité vers le bas)
et
min en a pour f'(a) = 0 et f"(a) > 0 (car concavité vers le haut)

ici : f''(x) = 36x²-12

f"(0)=-12 < 0 donc x=0 est un max
f"(1) = 24 > 0 donc x=1 est un min
f"(-1)=24 > 0 donc x=-1 est un min


cela te va ?

à bientôt !