Inscription / Connexion Nouveau Sujet
Trouver une dimension afin d'obtenir un volume maximal
Bonjour,
Je suis bloquée à un endroit de mon exercice et je me permets de solliciter votre aide.
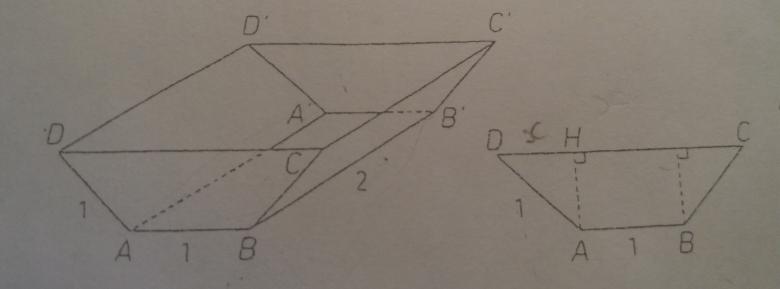
Voici l'énoncé (Je mettrais le schéma ensuite): Un abreuvoir a la forme d'un prisme droit dont la base est un trapèze isocèle ABCD. Toutes les dimensions sont fixées sauf la longueur CD. L'unité est le mètre.
Déterminer la dimension à donner à la grande base (CD ) du trapèze afin que le volume du récipient soit maximal.
J'ai donné une expression de HA avec Pythagore et J'ai trouvé racine de 1-x2
Ensuite J'ai donné une expression pour l'aire du trapèze J'ai trouvé (2x+2) * racine de 1-x2 /2
Ensuite j'ai donné une expression pour le volume de l'abreuvoir et j'ai trouvé (2x+2)*racine de 1-x2
Puis pour trouver la dimension de CD pour que le volume du récipient soit maximal j'ai calculé la dérivée du Volume et cela m'a donné -8x2-4x+4 / 2*racine de 1-x2
C'est ici que je suis bloquée car je ne sais pas si j'ai bon et je ne parviens pas à faire le tableau de variations (C'est la racine au dénominateur qui me gêne)
Merci d'avance
Ce radical en dénominateur est toujours positif et n'intervient donc pas dans le signe de la dérivée.
Ce radical en dénominateur est toujours positif et n'intervient donc pas dans le signe de la dérivée.
Ah oui effectivement merci! Mais doit on faire apparaître les valeurs interdites dans le tableau pour ce dénominateur? C'est à dire toutes les valeurs égales et supérieure à à 1 et inférieures à 0? Ou alors x doit être compris entre 0 et 1?
Oui, x doit être compris entre 0 et 1 pour que l'expression sous le radical soit positive, mais 1 étant exclu car, si x était égal à 1 , le dénominateur de la dérivée s'annulerait.
1 est donc valeur interdite pour x .
Oui, x doit être compris entre 0 et 1 pour que l'expression sous le radical soit positive, mais 1 étant exclu car, si x était égal à 1 , le dénominateur de la dérivée s'annulerait.
1 est donc valeur interdite pour x .
Encore merci pour votre aide! Ainsi, les valeurs que je fais apparaître dans le tableau pour x sont 0 ; 0,5 (qui annule le numérateur de la dérivée en 0) et 1 (en précisant bien que c'est une valeur interdite avec la double barre)