Niveau autre

Un exercice qui porte essentiellement sur les complexes

Posté par Guizmo (invité) 17-09-05 à 21:40

Bonjour à tous. C'est mon premier message alors veuillez m'excuser pour les quelques éventuels écarts
Alors voilà j'ai un exo de maths que je n'arrive pas à résoudre. Je vais d'abord noter "l'intro" de l'exercice :
On note U_n l'ensemble des points du plan complexe P ayant pour affixe un élément de U_n (ce dernier U_n est différent il désigne l'ensemble des complexes de module 1, en fait c'est pratiquement la même chose allez comprendre ma prof ) et l'on pose, pour tout z,f(z)=(z²+z+²)
avec U_n
Alors maintenant les questions :
1) Déterminer les nombres complexes z et z' sachant que module(z)=module(z')=1 et module(1+z+z')=3
2)a)Soit U_n. Montrer que l'application :/ est une bijection de U_n dans lui même.
b)Montrer que l'application :³ est une bijection de U_n dans lui même
3)On note V_n (respectivement W_n) l'ensemble obtenu en transformant U_n par la rotation de centre O et d'angle 2/3 (respec -2/3)
Pour tout point M du cercle unité C, on pose F(M)=(M) avec V_nW_n
a)Montrer que V_n et W_n sont disjoints
b)Montrer que, pour tout MC, F(M)3
c)Déterminer les points MC pour lesquels F(M)=3
Je sais que j'en demande beaucoup pour des personnes déjà occupées, mais je ne demanderais pas si je n'étais pas si désespéré.
A vrai dire je crois que j'ai trouvé la question 1) au moins : z=z'=1 mais pour le reste...
S'il vous plait aidez moi...

Posté par Guizmo (invité)re : Un exercice qui porte essentiellement sur les complexes 17-09-05 à 21:59

Euh juste une petite précision je dois rendre ça pour lundi. Je veux pas avoir l'air exigeant mais bon...
Enfin merci à tous ceux qui pourront m'aider.

Posté par re : Un exercice qui porte essentiellement sur les complexes 18-09-05 à 03:35

Bonsoir Guizmo;non tu n'est pas exigeant et n'hésites pas à poser les questions qui te désespérent on est là pour répondre.
Au début,je crois que tu as oublié de mentionner que:
* $n$ est un entier naturel non multiple de $3$ .
* $U_n=\{z\in\mathbb{C}/z^n=1\}$ .
Pour éviter toute confusion (m^me si quelques professeurs emploient la mm notation)on notera
$\mathbb{U}_n=\{M(z)/z^n=1\}$ .
1/
$\fbox{|z|=|z'|=1\\|1+z+z'|=3}$ $\Longleftrightarrow$ $\fbox{z=z'=1}$ (ta réponse est juste mais tu n'as pas dit comment tu l'as montré)
J'en donne une démonstration géomètrique:
on a $\fbox{|z|=|z'|=1\\|\frac{z+z'}{2}-(-\frac{1}{2})|=\frac{3}{2}}$ ainsi si on note $A,B,M,M'$ et $I$ les points d'affixes respectifs $1,-\frac{1}{2},z,z'$ et $\frac{z+z'}{2}$ les relations précédentes se traduisent par:
* $M$ et $M'$ sont sur le cercle $C(O,1)$ (dit aussi cercle unité).
* leur mileu $I$ est sur le cercle $C'(B,\frac{3}{2})$ .
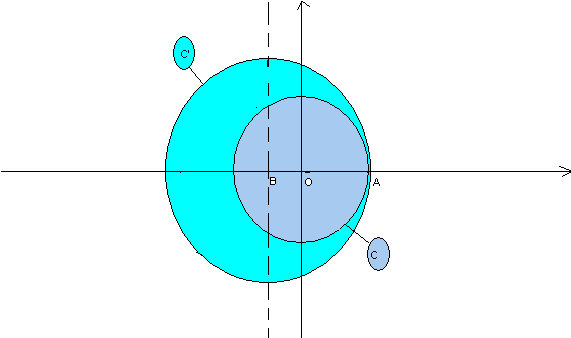
il est facile de voir que ces deux cercles sont tangents extérieurement en $A$ (voir image attachée).
on voit alors que $\fbox{z=z'=1}$
2/
a) pour $\alpha,\beta\in U_n$ on a bien $(\frac{\alpha}{\beta})^n=\frac{{\alpha}^n}{{\beta^n}}=\frac{1}{1}=1$ donc $\frac{\alpha}{\beta}\in U_n$ en plus l'application $\psi_\beta$ est clairement injective donc bijective puisque l'ensemble de départ et d'arrivée sont finis et ont mm cardinal.
b) de mm on a pour tout $\alpha\in U_n$ $(\alph^3)^n=(\alph^n)^3=1$ donc l'application $\phi$ est bien définie et elle est injective car si $\phi(\alpha)=\phi(\alpha')$ alors $(\frac{\alpha}{\alpha'})^3=1$ ce qui veut dire que $\frac{\alpha}{\alpha'}\in\{1,j,j^2\}$ où $j=e^{\frac{2i\pi}{3}}$ et comme $\fbox{et\{{j^n\neq1\\j^{2n}\neq1}$ (puisque n n'est pas multiple de $3$ ) il vient que $\alpha=\beta$ et on a ainsi que $\phi$ est bijective.
je me contenterais de ça pour le moment car il est tard et je dois me coucher mais ne t'en fait pas je ferais un autre post demain si c'est nécéssaire.
Amicalement elhor

Un exercice qui porte essentiellement sur les complexes

Posté par Guizmo (invité)re : Un exercice qui porte essentiellement sur les complexes 18-09-05 à 10:27

pour la question une, j'ai d'abord dit que z,module(z)=(z* $\bar{z}$ ) donc module(1+z+z')=((1+z+z')* $\bar{1+z+z'}$ ), j'ai mis ça au carré, j'ai développé et je suis tombé sur cos()+cos()+cos(-)=3 avec et les arguments de z et z'. De là sachant qu'il n'y a qu'une valeur de et pour lequel cos s'annule (soit 0) j'ai trouvé qu'ils étaient confondus.
En tout cas merci BEAUCOUP pour ce début de réponse.

Posté par Guizmo (invité)re : Un exercice qui porte essentiellement sur les complexes 18-09-05 à 10:29

Oups erreur dans le message précédent "il n'y a qu'une valeur de et pour lequel cos = 1 (modulo 2 bien sûr)"

Posté par re : Un exercice qui porte essentiellement sur les complexes 18-09-05 à 12:35

Bonjour Guizmo;
Ta réponse pour le début de la question 1/ est juste.Effectivement avec $z=e^{i\theta}$ et $z'=e^{i\theta'}$ on a
$9=(1+z+z')\bar{1+z+z'}=3+z+\bar{z}+z'+\bar{z'}+z\bar{z'}+\bar{z}z'$
d'où: $cos(\theta)+cos(\theta')+cos(\theta-\theta')=3$
d'où $\underb{(1-cos(\theta))}_{\ge0}+\underb{(1-cos(\theta'))}_{\ge0}+\underb{(1-cos(\theta-\theta'))}_{\ge0}=0$
d'où $\theta,\theta'\in2\pi\mathbb{Z}$ et par conséquent $z=z'=1$ .
3/a)
soient $\fbox{M(z)\in V_n\\M'(z')\in W_n}$ donc $\fbox{(\exists\alpha\in U_n)\hspace{5}/\hspace{5}z=j\alpha\\(\exists\beta\in U_n)\hspace{5}/\hspace{5}z'=j^{2}\beta}$ et comme $\fbox{\forall\alpha,\beta\in U_n\\j\alpha\neq j^{2}\beta}$ puisque $\fbox{j^n\neq1}$ on voit que les ensembles $V_n$ et $W_n$ sont disjoints.
Avant d'attaquer le $3/b)$ retenons que:
$2$\fbox{V_n=\{M(j\alpha)\hspace{5}/\hspace{5}\alpha\in U_n\}\\W_n=\{M(j^{2}\alpha)\hspace{5}/\hspace{5}\alpha\in U_n\}}$ et que $2$\fbox{\forall z\in\mathbb{C}\\ \Bigprod_{\alpha\in U_n}(z-\alpha)=z^n-1}$
3/b)
soient $z,z'$ les affixes respectifs des points $M$ et $F(M)$ on peut écrire:
$2$\fbox{|z'|=\Bigprod_{\alpha\in U_n}|z-j\alpha|\times\Bigprod_{\alpha\in U_n}|z-j^{2}\alpha|=\Bigprod_{\alpha\in U_n}|\frac{z}{j}-\alpha|\times\Bigprod_{\alpha\in U_n}|\frac{z}{j^{2}}-\alpha|=| (\frac{z}{j})^{n}-1||(\frac{z}{j^2})^{n}-1|=|z^{n}-j^n||z^{n}-j^{2n}|}$
il suffit maintenant de remarquer que $2$\fbox{\{j^n,j^{2n}\}=\{j,j^2\}}$ et donc que les points d'affixes respectifs $1,j^n$ et $j^{2n}$ forment un triangle équilatéral.

Posté par re : Un exercice qui porte essentiellement sur les complexes 18-09-05 à 13:32

Continuons;
on a donc $\fbox{F(M)=|z'|=|z^n-j||z^n-j^2|=|z^{2n}-z^{n}(j+j^2)+j^3|= |z^{2n}+z^{n}+1|\le|z|^{2n}+|z|^{n}+1=3}$
remarque: $F(M)$ est un réel positif(puisque produit de distances) j'ai donc commis une belle étourderie en considérant son affixe mais faisons comme dit ta prof c'est pratiquement la mm chose
3/c)
on voit que $2$\fbox{F(M)=3\Longleftrightarrow|z^{2n}+z^{n}+1|=1}$ et en utilisant $1/$ on a que $z^n=1$ c'est à dire que $\fbox{z\in U_n}$ ou encore $2$\fbox{M(z)\in\mathbb{U}_n}$
Voilà,j'espére que c'est assez clair et à la prochaine.
Amicalement elhor

Posté par Guizmo (invité)re : Un exercice qui porte essentiellement sur les complexes 18-09-05 à 14:07

........
MERCI!!!!!!

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

géométrie en post-bac
4 fiches de mathématiques sur "géométrie" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Un exercice qui porte essentiellement sur les complexes

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths