Inscription / Connexion Nouveau Sujet
Un quadrilatère dans un autre
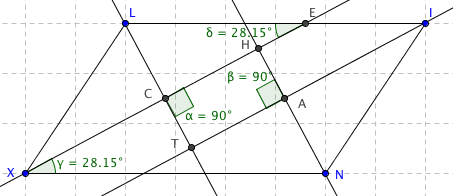
Soit. LINX un parralelogramme .Les bissectrices des angles du parralelogramme se coupent. 2 à 2,comme sur la figure ci-contre. a Reproduire une figure analogue ; bQuelle semble. Être la nature du quadrilatère CHAT? 2Obtient-on le même résultat si LINX est un rectangle?(réaliser une nouvelle figure ). 3Que dire de CHAT siLINX est un losange ?justifier. Aider moi svp!!
Bonjour à toi aussi
Il faudrait la figure pour savoir où se situent les points C, H, A et T, si tu ne peux pas la joindre donnes des explications
Bonjour,
Dans un parallélogramme, les angles opposés sont égaux.
Par conséquent, les demis angles le sont aussi
Par conséquent l'angle que la bissectrice issue de X fait avec la droite (LX) et l'angle que la bissectrice issue de I fait avec (VN)
sont en position d'alterne interne et égaux. Par conséquent les deux bissectrices sont parallèles
Il en est de même pour les bissectrices issues de L et N
et les 4 bissectrices forment donc un quadrilatère dont les côtés opposés sont //. c'est donc un parallélogramme
Si LINX est un rectangle, tu vois que deux bissectrices de 2 sommets consécutifs font entre eux un angle de 90° (si C est l'intersection des bissectrices issues de I et de X, le triangle ICX est un triangles dont deux angles en I et X valent 45°. Le 3ème angle de ce triangle vaut donc 90°)
le parallélogramme trouvé dans la question précédente sera donc un rectangle puisque les angles valent 90°
dans le cas du losange, tu sauras bien voir que toutes les bissectrices se coupent en un seul point car les diagonales du losange sont les bissectrices des angles au sommet
Définition
Soit O, A et B trois points.
La bissectrice de l'angle AÔB est la droite qui passe par le sommet O et qui partage l'angle AÔB en deux angles de même mesure.
Bonjour,
gaa : pas vraiment, il y a plus de propriétés que tu ne penses !
sinon, à permutation des points C, H, A, T près :
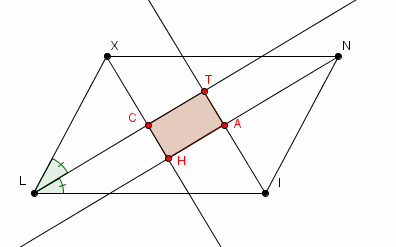
le problème c'est que pour causer de ces points il faudra bien savoir sur quelle bisectrice chacun se trouve !
("à permutation près", ais-je dit !)
grillé par Mijo (encore une fois, j'ai posté sans faire refresh)
qui en plus à donné la solution (enfin ce qu'il faut démontrer : que CHAT est un rectangle)
D'après toi ?
que faut il pour qu'il soit un rectangle ?
déja ce doit être un parallélogramme.
la figure de Mijo (ses angles de 28.15°) et les explications de gaa sont explicites : angles alternes internes et angles correspondants et c'est bon.
rappel : les angles opposés d'un parallélogramme (LINX) sont égaux.
les bisectrices coupent les angles en deux par définition.
ensuite il suffit de prouver qu'il a un angle droit
que peut on dire des angles du triangle LTI ?
rappel : les angles adjacents d'un parallélogramme sont supplémentaires
XLI + LIN = 180°.
donc TLI + LIT = ?
et par conséquent l'angle LTI ?
(avec les noms de ma figure ou de celle de Mijo. Sur la tienne les noms des points sont peut-être mélangé, ça ne change rien, tu adaptes)
gaa a déja tout dit pour prouver que c'est un parallélogramme. Tu veux que je recopie ?
pour l'angle droit, et si tu répondais à mes questions ?
pour la question 2 faire une figure, tu sais faire, quand même, non ?
qu'observes tu ?
Pour le démontrer il faut peut être s'intéresser aux diagonales du CHAT : les droites CA et HT.
Si on prouve qu'elle sont parallèles aux côtés de LINX c'est gagné : un rectangle (CHAT) qui a ses diagonales perpendiculaires est un carré.
donc on fait la chasse aux parallélogrammes dans la figure (ce n'est pas ce qui manque !)