Bonjour

Non, il s'agit vraiment d'une parabole, située dans le plan d'équation x+y=0.

Bonjour Camelia !
Oui, je suis d'accord, mais la justification me semble incorrecte.

Bonjour.

Pourquoi sur xOz ?

A priori, c'est une des dernières (voire la dernière) questions d'un exercice. Si tu mets le début de ta réponse (bien que fausse), on t'accorderait probablement tous les points...

Bonjour kioups ! (heureux que tant de monde me répondent)

Pourquoi sur xOz ?
>> Car on exprime z en fonction de x, on peut donc dire que si on regarde S en face du plan xOz on voit une parabole.

Mais ce n'est pas car, sous un certain angle, le rebord de mon verre est en forme d'ellipse que je peux en conclure que c'est une ellipse.

Bonjour,

ce type de questions dite "questions ouvertes" est un nouveau dada : on pose une question dont on est presque certain que l'élève moyen ne trouvera pas la réponse voire une question pour laquelle les outils du programme sont insuffisants.
Le but ? Apprendre aux élèves français à oser se lancer, proposer une solution incomplète ou n'aboutissant pas. On peut mettre tous les points (rarement plus de 2 au total sur un sujet) même face à une démarche fausse. L'idée est de valoriser un candidat prenant des initiatives, ayant des idées et pas seulement le candidat capable de suivre simplement la démarche du sujet.

Le vrai but ? Faire remonter la France dans les classements, pour lesquels les sujets comportent pas mal de questions de ce type. La même raison d'ailleurs qui a fait apparaitre les QCM aux bacs

En fait les outils du programme sont suffisant, mais il y a une telle différence de niveau entre les question "habituelle" du bac que ça fait vraiment bizarre.

Voici ce que j'aurais fait :

L'espace est muni d'un repère orthonormé .
Définissons un nouveau repère

Avec

On a ainsi :

d'où

Ainsi

Donc S est donc bien une parabole.

Heu bonjour,

j'ai fait cette annale à l'instant il n'y à pas de correction apparemment sur le site,

moi pour cette derniere question j'ai fais simple mais du coup je doute que ce soit valable en vue de ce que vous dites.

x+y=0

donc:

x=-y

or l'équation de S est telle que:



avec x=-y

z={y^2}{4}

Et c'est bien l'équation d'une parabole.

Bonjour numero10 !
En effet, je ne pense pas que ce soit valable, car il faut justifier que si la projection est une parabole alors c'est une parabole.
Il faut donc faire un changement de repère comme je l'ai fait.
Après comme la dit kioups, on te compterai tout les points même si la justification est fausse.

*pas fausse, mais insuffisante.

Oui je vois donc il me semble avoir déjà eu affaire à exercice comme ça.
Je vais y réfléchir mais cette exo sur les sections planes me parait quand même plus facile que les autres que j'ai eu à faire.

Bonjour,

alors ma réponse va peut être choquer

matovitch a raison : il ne faut surtout pas tomber dans le panneau parabole dans xOz ou yOz selon que l'on abandonne x ou y

D'ailleurs si y vaut zéro alors x et z aussi par la même occasion : si y=0 alors le point nul est la seule solution.

Non je pense qu'il faut simplement faire un dessin (selle de cheval), dire qu'on a un paraboloide hyperbolique (ça c'est le pgm) et donc que la section avec un plan vertical est une parabole par un petit schéma.

Puis la justification z=(1/4)x² avec y=-x càd qu'on a une parabole dans le plan vertical [x=-y]

A+

Pardon mariette a raison : attention surtout ne pas écrire y = 0

si y=0 alors x=z=0 et en effet le point nul est solution.

Mais tu ne dois pas te "prendre la tête": il faut simplement écrire:

z=(1/4)x² avec y=-x càd qu'on a une parabole dans le plan vertical [x=-y]

toute l'astuce est là : c'est dans le plan [y=-x]

et non justement tomber dans le panneau z=(1/4)x² et donc penser que la solution est dans xOz

je pense que c'était là la difficulté d'où les réserves en début d'énoncé

sasuser >>
Et justement, on ne sait pas à quoi correspond une tel système d'équation !
Ce que l'on peut juste et seulement dire c'est que la projection de sur parallèlement à est une parabole d'équation  .

D'ailleurs, On voit d'après le changement de repère que j'ai fait que l'équation dans le plan n'est pas la même.

or les veteur que j'ai pris sont fois plus grand.

D'où l'équation "à l'échelle" d'où ainsi .

Donc l'équation dans le plan est

Ce qui correspond bien à une affinité de direction rapport .

Logique car le plan forme un angle 45° avec on a donc l'équation de la parabole "tassée".

Donc est bien l'équation du projeté et pas l'équation dans le plan !

Vous avez raison : il faut bien préciser parabole par une transformation (je suis tombé dans le panneau):

par contre tant qu'à faire autant prendre un repère orthonormé:

Prenons le repère orthonormé :

I = (i - j)sqrt2/2
J = (i + j)sqrt2/2
K = k

et là on

X = 2(x-y)/sqrt(2)

Y = 2(x+y)/sqrt(2)

Z= z

soit pour Y=0; Z=(1/4)(2/16)X²=(1/32)X²

A+

Re-

J'ai repris l'équation un repère orthonormé dans mon post précédent.
Vous vous êtes trompés en remplaçant X et Y (c'est bizarre j'ai l'habitude de tutoyer sur ce forum).

bonjour,
une petite équation paramétrique de la parabole
x=t
y=-t
z=(1/4)t²

Salut Labo !
J'ai aussi pensé à l'équation paramétrique, mais ça n'est pas au programme de terminale.

bonjour matovitch
désolée , je ne connais pas les programmes....

Exercice très interessant.

A+

petite erreur :

bonjour
{z=(1/8)x² une surface  (rose)
{y=0  un plan (jaune
donc tu t'intéresses à leur intersection...
z=(1/4)x² une surface (bleue)
x+y=0  plan (vert)
et leur intersection...

salut, je ne comprend pas pourquoi on doit faire un changement de repère ici? et pourquoi parle-t-on de projection ?

en ayant , pourquoi ne peut-on pas dire directement qu'il s'agit d'une parabole située dans le plan d'equation x+y=0 ?

Bonjour,

Citation :

Pour être plus précis, on peut considérer l' équation:

comme l' équation d' un cylindre de génératrices parallèles à et, qui coupe le plan suivant la parabole d' équation dans le repère

Labo >>
Vu qu'on a fait un changement de variable, si tu fait tourner une intersection de 45° selon Oz (dans le bon sens) ça doit se superposer.

Stef >> Avec le système que tu donnes tu as une relation entre x et y et entre x et z.
Tu peux en déduire les projection de l'intersection sur xOy : droite d'équation .
Et sur xOz : parabole d'équation .
Mais tu ne peux rien déduire d'autre car tu n'as pas l'équation de dans le plan .
C'est pourquoi il faut faire un changement de variable pour déterminer cette équation.

Mais attention à ce que je dis car je ne suis qu'un élève de term comme toi, et c'est pourquoi j'aimerai bien qu'un(e) prof donne son avis.
_{nb : je suis quand même assez sûr de moi}

Au fait bonsoir Stef et cailloux !

matovitch
j'ai zappé le changement de variables...

Labo >>

cailloux >>

Citation :
comme l' équation d' un cylindre de génératrices parallèles à et, qui coupe le plan suivant la parabole d' équation dans le repère

salut matovitch, tu veux dire la projection orthogonale de l'intersection entre S et le plan d'eq x+y=0, non? sinon, je ne capte plus rien (et merci, avec ton explication + celle de cailloux, je pense avoir compris, mais si tu répond non à ce que je viens de te dire j'aurais compris tout de travers )

mais j'ai bien peur que tu parles bel et bien de la projection de S sur xOz, et alors je suis complètement perdu. ;(

Euh oui, j'ai dit une co... je pensais à l'intersection bien sûr !

Re,

>> matovitch

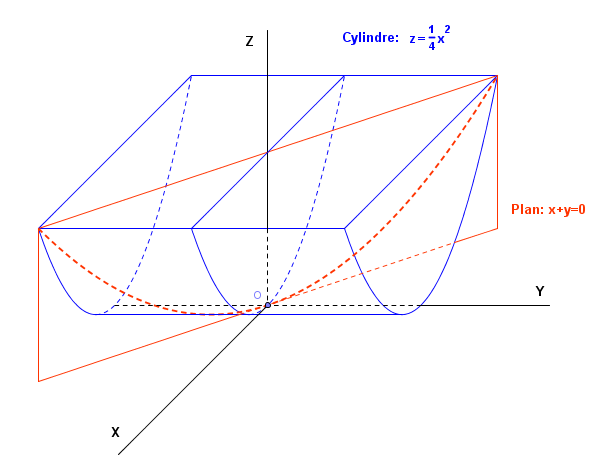
Un dessin pour illustrer 20h47.

La courbe intersection cherchée est la courbe en pointillés rouges du plan d' équation

C' est la parabole intersection du cylindre (l' auge à cochons dessinée en bleu) d' équation et du plan d' équation

Re-

>> On est d'accord !
"cylindre"(le terme me parraissait bizarre car je pensais que tout les cylindre étaient rond)
Sinon, on ne peut pas parles de génératrice pour un cylindre parabolique car une génératrice est l'axe selon lequel pivote la courbe pour former la surface.
On dit donc que c'est un cylindre parabolique dont la directrice est la parabole d'équation .

Les définitions de cylindre sont variables...

En voici une qui correspond à ce que j' ai écrit plus haut:

En effet, celle que j'avais trouvé étais sur wiki...
Bref, je pense que tu as raison.

J'ai aussi trouvé ça sur wiki :